本节讨论一组随机变量联合分布的图模型的基本性质。而关于参数化和从样本数据中估计边的参数,以及对一个图的拓扑的估计,将会在后续章节介绍。
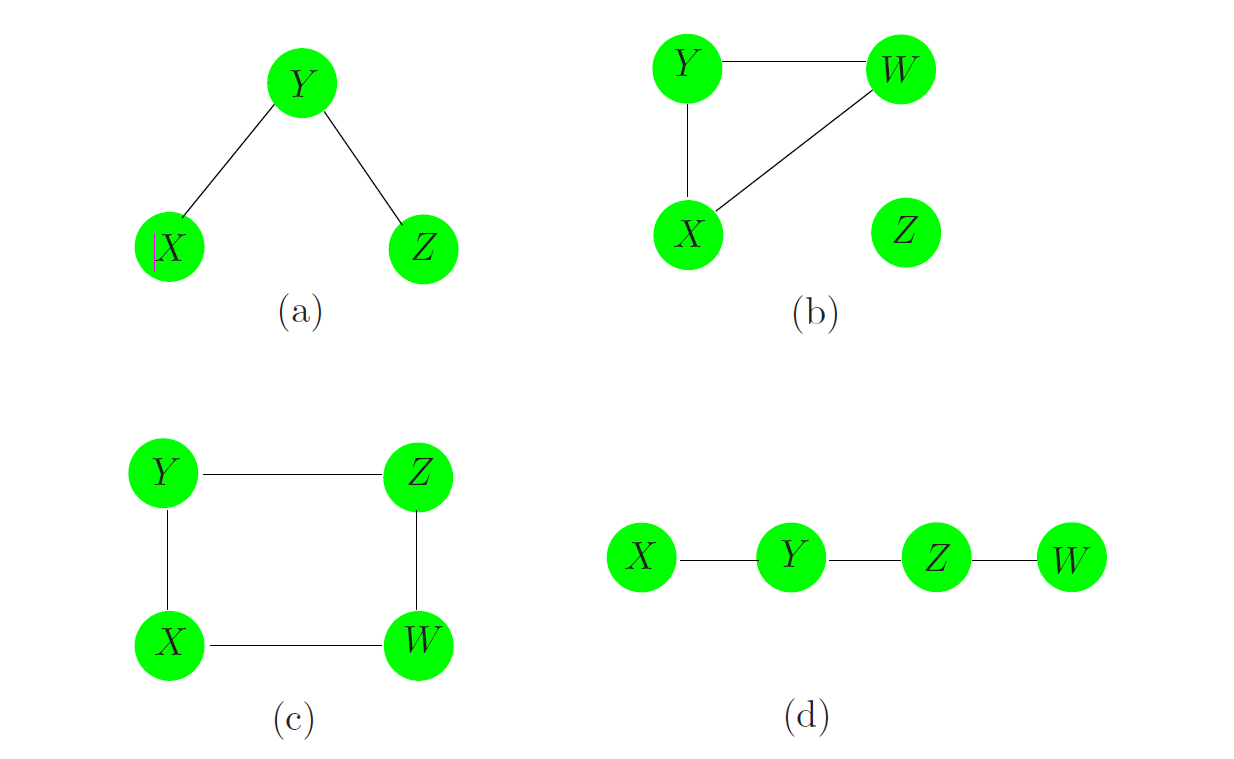
图 17.2 展示了四个无向图的例子。一个图 $\mathcal{G}$ 有两个组成元素 $(V,E)$,其中的 $V$ 是顶点(vertex)的集合,而 $E$ 是边(edge)的集合;边的定义是两个顶点的点对。如果两个顶点 $X$ 和 $Y$ 之间存在一个连接着它们的边,则称这两个顶点是 邻接(adjacent) 的;记作 $X\sim Y$。一组依次连接着的顶点 $X_1,X_2,\dots,X_n$ 被称为一个路径,即满足 $X_{i-1}\sim X_i,i=2,\dots,n$。当一个图中的所有顶点两两之间都被一个边连接,那么这个图就是一个 完全图(complete graph)。顶点的一个子集 $U\subset V$ 以及它们之间的边,形成了一个 子图(subgraph)。例如,图 17.2(a)中的 $(X,Y,Z)$ 构成了一个路径,但不是一个完全图。
假设在一个图 $\mathcal{G}$ 中,其顶点集合 $V$ 代表了联合分布为 $P$ 的一组随机变量。在一个马尔科夫图 $\mathcal{G}$ 中,两个顶点之间不存在边就意味着两个对应的随机变量在条件于其他顶点对应的随机变量下是独立的。这可用以下的符号来表达:
$$X \text{ 和 } Y \text{ 之间没有连接的边} \longleftrightarrow X \perp Y |\text{其他变量} \tag{17.1}$$其中的“其他变量”指的是图中所有其他的顶点。例如在图 17.2(a)中,$X\perp Z|Y$。这被称作为在 $\mathcal{G}$ 中 两两之间马尔科夫独立(pairwise Markov independencies)。
如果 $A$、$B$、和 $C$ 为三个子图,如果 $A$ 和 $B$ 之间的每一条路径都需要经过 $C$ 中的一个顶点,那么就可以说 $C$ 分隔(separate) 了 $A$ 和 $B$。例如在图 17.2 中,$Y$ 在(a)和(d)中分隔了 $X$ 和 $Z$,$Z$ 在(d)中分隔了 $Y$ 和 $W$。在(b)中, $Z$ 与 $X$、$Y$、和 $W$ 都不连接,所以可以说这两组顶点被空集分隔。在(c)中,$C=\{X,Z\}$ 分隔了 $Y$ 和 $W$。
分隔子图有一个很好的性质,它们将可以将一个图分成条件独立的组成部分。具体来说,一个马尔科夫图 $\mathcal{G}$ 有三个子图 $A$、$B$、和 $C$:
$$\text{如果 } C \text{ 分隔了 } A \text{ 和 } B \text{,那么 }A \perp B | C \tag{17.2}$$这就是图 $\mathcal{G}$ 的 全局马尔科夫性质(global Markove properties)。可证明(对于正分布的图)两两之间和全局马尔科夫性质是等价的。也就是说,满足两两之间马尔科夫独立和全局马尔科夫性质的概率分布所对应的图的集合是相同的。这个结论可用于从简单的两两性质来推断全局的独立关系。例如在图 17.2(b)中,因为这是一个马尔科夫图并且在 $X$ 和 $Z$ 之间没有连接的边,所以 $X\perp Z|\{Y,W\}$。而同时 $Y$ 也分隔了 $X$ 和 $\{Z,W\}$,所以根据全局马尔科夫性质,可知 $X\perp Z|Y$ 以及 $X\perp W|Y$。类似地,也可得出 $Y\perp W|Z$。
全局马尔科夫性质让我们可以将一个图分解成更小更容易处理的组成部分,所以可以得到在计算量和可解释性上必要的简化。所以我们会把一个图分成一些“团”。一个 团(clique) 是一个完全的子图:一组两两都邻接的顶点的集合。如果一个团在加入任意的顶点后都不再继续是团,那么就称这个团为 极大团(maximal clique)。图 17.2 中每个图的极大团如下:
- (a):$\{X,Y\}, \{Y,Z\}$
- (b):$\{X,Y,W\}, \{Z\}$
- (c):$\{X,Y\}, \{Y,Z\}, \{Z,W\}, \{X,W\}$
- (d):$\{X,Y\}, \{Y,Z\}, \{Z,W\}$
虽然下面的公式在连续和离散的分布都适用,不过大部分的研究是针对离散分布的。一个马尔科夫图 $\mathcal{G}$ 上的概率密度函数 $f$ 可写为:
$$f(x) = \frac{1}{Z} \prod_{C\in\mathcal{C}} \psi_C(x_C) \tag{17.3}$$其中的 $\mathcal{C}$ 为极大团的集合,正值函数 $\psi_C(\cdot)$ 被称为 团势(clique potential) 函数。这些函数一般并不是密度函数1,而是一种通过对 $x_C$ 的不同赋值来体现 $X_C$ 中的相关性的亲和函数。
$$Z = \sum_{x\in\mathcal{X}} \prod_{C\in\mathcal{C}} \psi_C(x_C) \tag{17.4}$$数量 $Z$ 是标准化常量,也被称作 配分函数(partition function)。从另一角度也可以认为,表达式 17.3 意味着一个带有独立性质的团可由乘积中的团来定义。这个结果对正数分布的马尔科夫网络 $\mathcal{G}$ 成立,即为 Hammersley-Clifford 定理(Hammersley and Clifford, 1971;Clifford, 1990)。
很多图模型的估计和计算方法都先将图分解成它的极大团。在每个团上各自地计算相关的数值,然后再汇总到整个的图模型。一个明显的例子从一个图的联合分布中计算出边界和低阶概率分布的 连接树(join tree) 或 联合树(junction tree) 算法。具体细节可参考 Pearl (1986)、Lauritzen and Spiegelhalter (1988)、Pearl (1988)、Shenoy and Shafer (1988)、Jensen et al. (1990)、以及 Koller and Friedman (2007)。
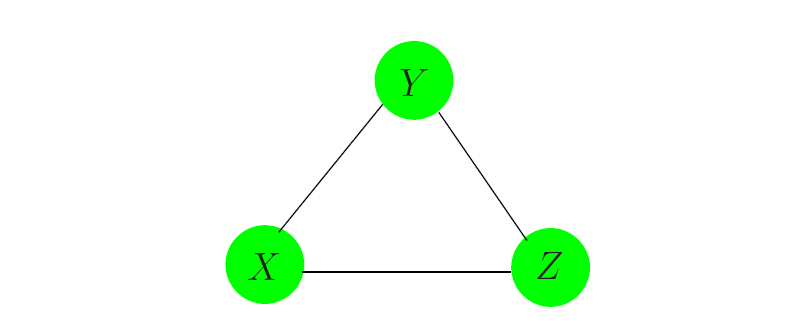
一个图模型并不总会唯一地表达一个联合概率分布的高阶相关结果。以图 17.3 中的三个节点的完全图为例。它可以同时代表以下两个概率分布的相关性结构:
$$\begin{align} f^{(2)}(x,y,z) &= \frac{1}{Z} \psi(x,y) \psi(x,z) \psi(y,z) \\ f^{(3)}(x,y,z) &= \frac{1}{Z} \psi(x,y,z) \end{align}\tag{17.5}$$第一个函数只表达了二阶相关性(并且可用更少的参数来表示)。离散数据的图模型是 多维列联表的对数线性模型(loglinear models for multiway contingency tables) 的一个特例(可参考 Bishop et al., 1975);在多维列联表的术语中,$f^{(2)}$ 被看作为“无二阶交互”(no second-order interaction)模型。
本章的后续内容将集中于两两马尔科夫图(Koller and Friedman, 2007)。它们的每个边(如上式 $f^{(2)}$ 中的两两变量对)都有一个团势函数,并且最高只考虑二阶的交互。这样的做法在参数上更简约,也更容易处理,并且是图结构复杂度最低的表达方式。于是连续和离散数据的模型都是只由边集合中的变量的两两边际分布组成的函数。
本节练习
练习 17.1
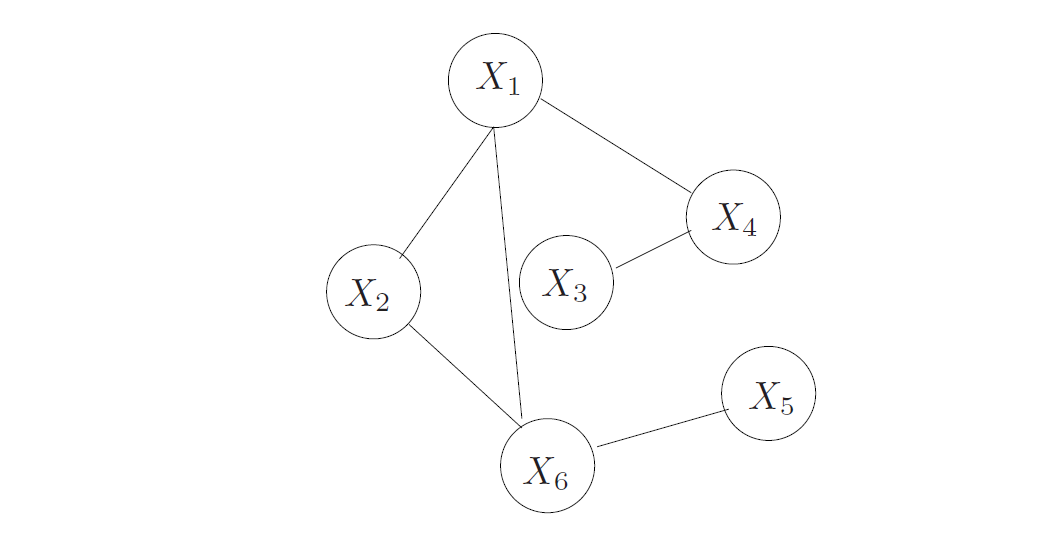
列出 图 17.8 中马尔科夫图的所有条件独立关系,以及它的极大团。
练习 17.2
假设有四个随机变量 $X_1$、$X_2$、$X_3$、$X_4$。画出满足以下每个独立相关性结构的图模型。
- $X_1\perp X_3|X_2$ 和 $X_2\perp X_4|X_3$
- $X_1\perp X_4|X_2,X_3$ 和 $X_2\perp X_4|X_1,X_3$
- $X_1\perp X_4|X_2,X_3$、$X_1\perp X_3|X_2,X_4$ 和 $X_3\perp X_4|X_1,X_2$
练习 17.4
令函数
$$f(X_1 | X_2, X_3, \dots, X_p)$$代表给定 $X_2,\dots,X_p$ 下 $X_1$ 的条件密度函数。如果:
$$f(X_1 | X_2, X_3, \dots, X_p) = f(X_1 | X_3, \dots, X_p)$$证明 $X_1\perp X_2|X_3,\dots,X_p$。
-
原文脚注 1:如果这些团是彼此分隔的,那么团势函数就可以是密度函数,不过一般来说并不会是这样的情况。 ↩︎