近期提出了一些用于非线性降维的方法,它们与主曲面的原理类似。其想法是数据样本通常在本质上分布在一个嵌在高维空间中的低维非线性流形的附近。这些方法可被看作是在将这个流形扁平化,所以可以把数据降维到一个能够表达它们在流形上的相对位置的低维坐标系上。它们在信号噪声比高的问题中比较有效(例如,物理学系统),但可能在比较低的信号噪声比的观测样本数据中不太有效。

图 14.44 的左图演示了降维问题的基本目标。一些数据分布在一个曲度较大的抛物线附近。经典的多维尺度(MDS)方法不会保留这些数据点之间沿着曲线的顺序,而会认定在曲线两端的点是互相接近的点。右图展示了 局部多维尺度(local multi-dimensional scaling) 的结果,它是下面即将介绍的三个非线性多维尺度方法之一。这些方法只会用到这些数据点在 $p$ 维上的坐标,而没有其他关于流形的信息。局部尺度分析很好地保持了这些数据点沿着曲线的顺序位置。
接下来将简要地介绍用于非线性降维和流形映射。
等距特征映射(isometric feature mapping, ISOMAP)(Tenenbaum et al., 2000)构建了一个图结构用于近似数据点之间沿着流形的测地线(geodesic)距离。具体来说,为每一个数据点寻找它的邻域点,即距离这个点某个小欧式距离范围内的数据点。邻域中的所有点之间都用一条边(edge)连接,从而构建了一个图结构。然后可将任意两个点之间的测地线距离近似定义为在图结构上能够连接两个点的最近路径。最后,在这个图结构定义的距离上应用经典的多维尺度方法,从而得到一个低维的映射。
局部线性嵌入(local linear embedding,LLE)(Roweis and Saul, 2000)采取了一个非常不同的方式,设法要保留高维数据样本中的局部仿射(或线性,affine)结构。将每个数据用它的邻域点的一个线性组合来近似。然后构建一个可最大程度保留这些局部近似的低维表达形式。这个过程比较有趣,所以我们给出计算细节如下。
- 对 $p$ 维空间上的每个数据点 $x_i$,寻找它的欧式距离 $K$ 最近邻 $\mathcal{N}(i)$。
- 对每个数据点,用它邻域中的点的一个线性组合来进行近似: $$\min_{w_{ik}} \|x_i - \sum_{k\in\mathcal{N}(i)} w_{ik} x_k\|^2 \tag{14.102}$$ 最小化针对的是权重 $w_{ik}$,满足条件 $w_{ik}=0,k\notin\mathcal{N}(i)$ 和 $\sum_{k=1}^Nw_{ik}=1$。$w_{ik}$ 是点 $k$ 在重构点 $i$ 中的贡献值。请注意若想要得到唯一的解,需要满足 $K<p$。
- 最后,固定 $w_{ik}$ 后对下式进行最小化,得到维度 $d<p$ 空间上的点 $y_i$: $$\sum_{i=1}^N \|y_i - \sum_{k=1}^N w_{ik} y_k\|^2 \tag{14.103}$$
在第 3 步中,最小化的准则函数为:
$$\operatorname{tr}[ (\mathbf{Y}-\mathbf{W}\mathbf{Y})^T(\mathbf{Y}-\mathbf{W}\mathbf{Y})] = \operatorname{tr}[ \mathbf{Y}^T(\mathbf{I}-\mathbf{W})^T(\mathbf{I}-\mathbf{W})\mathbf{Y}]$$ $$\tag{14.104}$$其中的 $\mathbf{W}$ 为 $N\times N$;$\mathbf{Y}$ 为 $N\times d$,$d<p$ 是一个小的维度。最小化的解 $\hat{\mathbf{Y}}$ 是矩阵 $\mathbf{M}=(\mathbf{I}-\mathbf{W})^T(\mathbf{I}-\mathbf{W})$ 的后几个本征向量。由于 $\mathbf{1}$ 是本征值 0 对应的本征向量平凡解,所以需要跳过这个本征向量,取接下来的 $d$ 个。这也会使得 $\mathbf{1}^T\mathbf{Y}=0$,所以嵌入坐标是已经均值中心化的。
局部多维尺度(local MDS)(Chen and Buja, 2008)采取了最简单的,并也可以说是最直接的方法。定义 $\mathcal{N}$ 为对称的邻近点对的集合;具体地说,只有当点 $i$ 是点 $i’$ 的 $K$ 最近邻并且反之也是,点对 $(i,i’)$ 才被包括在 $\mathcal{N}$ 中。然后构建一个应力函数(stress function):
$$\begin{align} S_L(z_1, z_2, \dots, z_N) &= \sum_{(i,i') \in \mathcal{N}} (d_{ii'} - \|z_i-z_{i'}\|)^2 \\ &+ \sum_{(i,i') \notin \mathcal{N}} w \cdot (D - \|z_i-z_{i'}\|)^2 \tag{14.105}\end{align}$$其中的 $D$ 是一个大的常数,$w$ 为一个权重值。这个结构的想法是将不相邻的点视为彼此之间距离很远,同时也给这些点对赋予一个小的权重 $w$ 使它们不会完全控制了整个应力函数。为简化这个表达式,令 $w\sim1/D$ 并且 $D\to\infty$。将式 14.105 展开,可得到:
$$\begin{align} S_L(z_1, z_2, \dots, z_N) &= \sum_{(i,i') \in \mathcal{N}} (d_{ii'} - \|z_i-z_{i'}\|)^2 \\ &- \tau \sum_{(i,i') \notin \mathcal{N}} \|z_i-z_{i'}\| \tag{14.106}\end{align}$$其中的 $\tau=2wD$。式 14.106 中的第一项是想要保留数据中的局部结构,而第二项则促进了把不相邻的点对 $(i,i’)$ 重构为较远的 $z_i$ 和 $z_{i’}$。局部多维尺度固定住邻域个数 $K$ 和调节参数 $\tau$ 后对应力函数(式 14.106)针对 $z_i$ 进行最小化。
图 14.44 的右图展示了局部多维尺度的结果,其中使用了 $k=2$ 个邻域并且 $\tau=0.01$。为了寻找到(非凸)应力函数式 14.106 的最小值点,我们在多个起始点应用了坐标下降方法。数据点沿着曲线的顺序位置被很大程度地保留了下来。
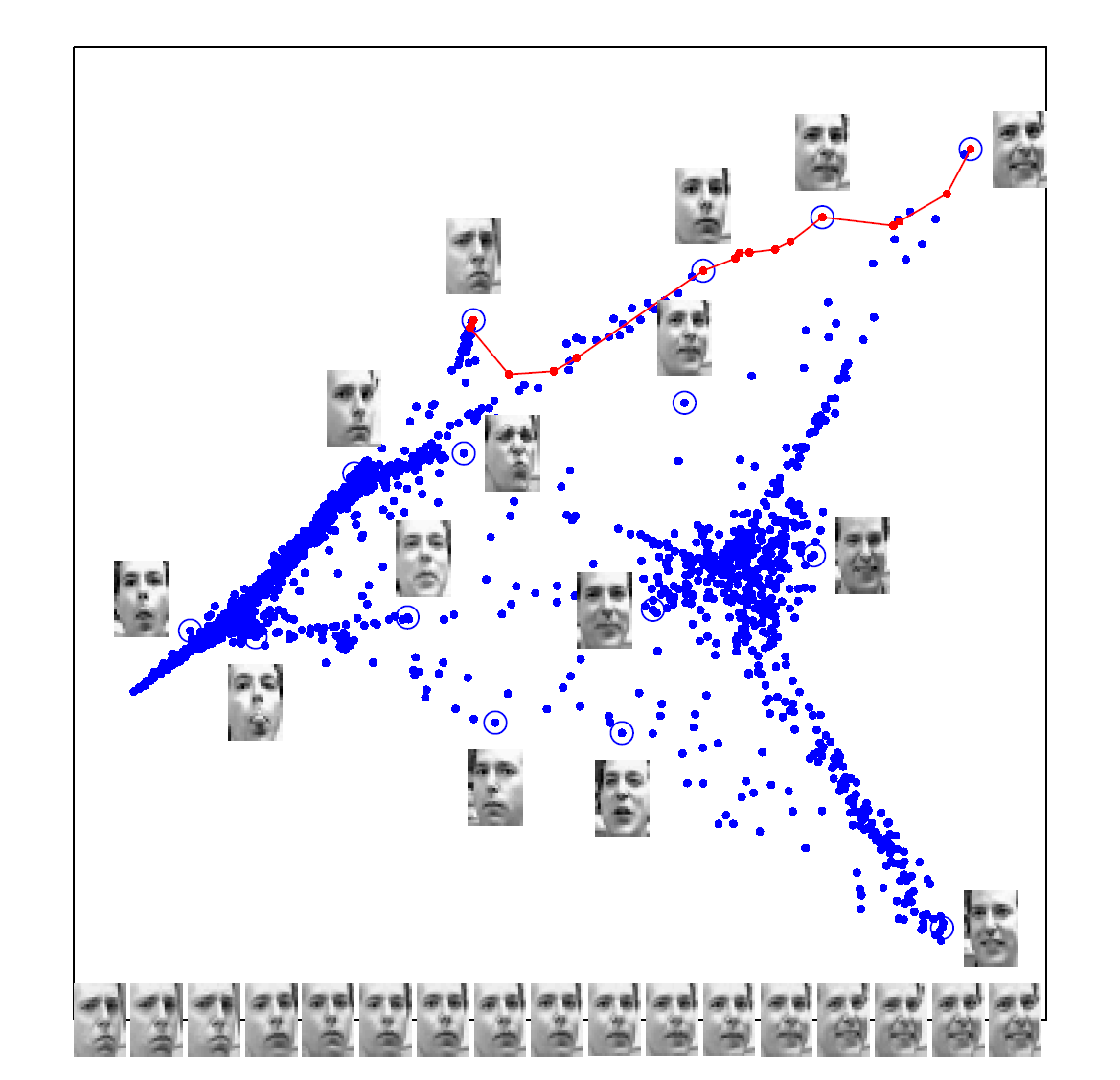
图 14.45 演示了这几个方法之一(LLE)的一个更有趣的应用1。数据包含了 1965 个照片,照片被数字化为 $20\times28$ 的灰度图片。图中展示了 LLE 前两个坐标的结果,并展现出了在姿势和表情上的一些变化。局部 MDS 也可得到类似的结果。
在 Chen and Buja (2008) 的实验结果中,局部 MDS 的表现明显好于 ISOMAP 和 LLE。他们也演示了局部 MDS 在图片布局上的有效应用。最后,本节讨论的方法与谱聚类(spectral clustering,第 14.5.3 节)和核主成分(kernel PCA,第 14.5.3 节)有紧密的关联。
-
原文脚注 15:Sam Roweis and Lawrence Saul kindly provided this figure. ↩︎