这类分类器是基于记忆的(memory-based),并且不需要对模型拟合。给定一个代分类的点 $x_0$,我们找出训练集中与 $x_0$ 距离最近的 $k$ 个点 $x(r),r=1,\dots,k$,然后用这 $k$ 个近邻的多数投票结果作为分类。若出现平局则随机决定。简单起见,我们将假设特征为实数取值的,并且在特征空间上使用欧式(Euclidean)距离:
$$d_{(i)} = \|x_{(i)} - x_0\| \tag{13.1}$$一般我们会首先将每个特征变量标准化为均值零和方差一,因为它们可能是不同单位下的测量值。第十四章会介绍适用于定性和有序的特征变量的距离测度,以及如何在(定量和定性)混合数据中使用它们。本章后面部分会介绍自适应地选择距离测度。
尽管形式很简单,k 最近邻在很多分类问题中都非常有效,例如手写数字识别、卫星图片识别、和心电图(EKG)模式识别。它通常在每个类别可能有多个原型而且决策边界非常不规则的问题中非常有效。图 13.3(上图)展示了应用在三个类别的模拟数据上的 15 最近邻分类器的决策边界。与下图的 1 最近邻分类器相比,这个决策边界是相对平滑的。最近邻和原型方法之间有密切的联系:在 1 最近邻分类模型中,每个训练样本都是一个原型。
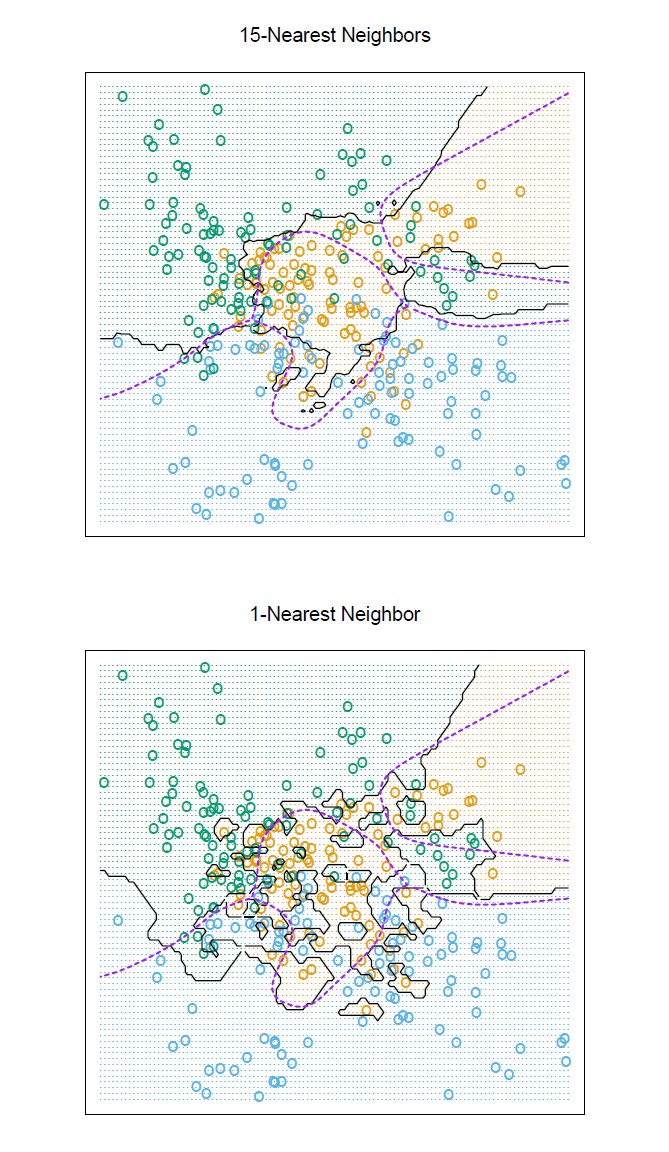
图 13.4 展示了在两个类别的混合数据问题中,训练、测试、和十折交叉验证误差率对近邻大小的函数曲线。十折交叉验证误差率来自十个数字的平均,所以也可估计它的标准差。
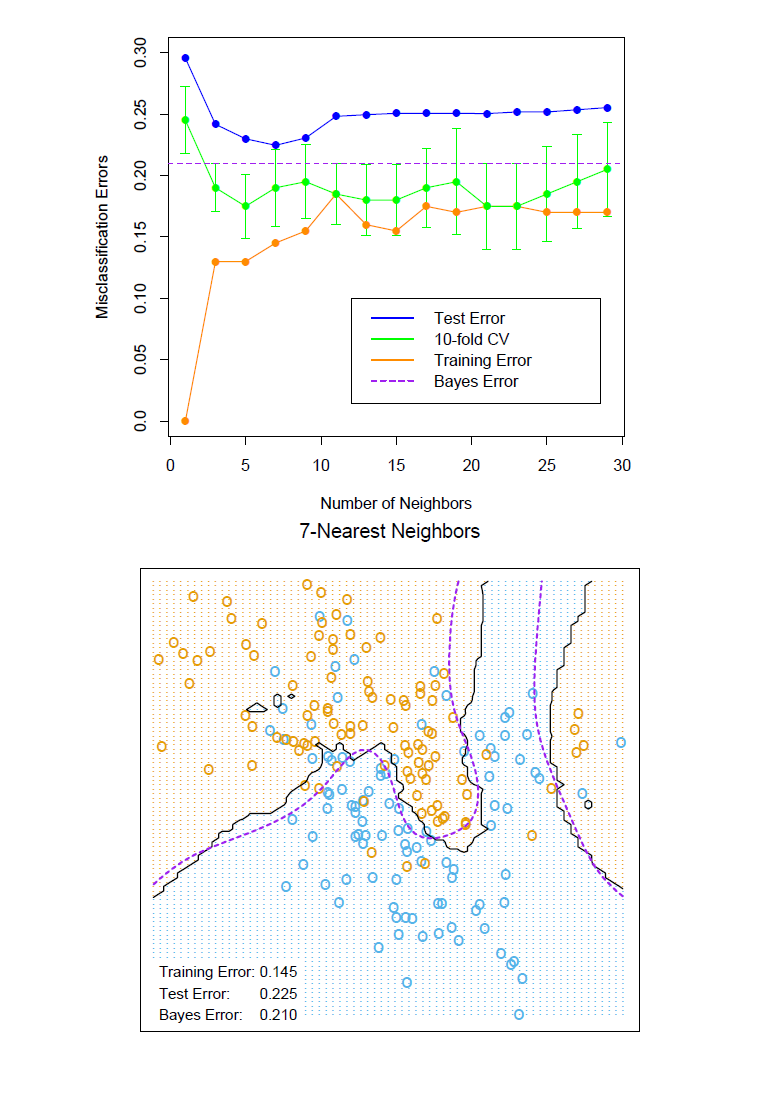
考虑 1 最近邻,由于它只使用距离待分类点距离最近的几个训练样本点,其估计结果的偏差通常比较低,但方差比较高。Cover and Hart (1967) 的一个著名的结果证明了 1 最近邻分类器的渐进误差率总不大于贝叶斯误差率的两倍。证明的大体思路如下(使用了平方误差损失函数)。假设待分类点与某个训练样本点重合,则偏差为零。如果特征空间的维度固定,则当训练样本密集地填满整个特征空间时(即渐进条件 $N\rightarrow\infty$),这是成立的。那么贝叶斯分类规则的误差为一个伯努利随机变量(待分类点的输出变量)的方差,而 1 最近邻分类规则的误差为两个伯努利随机变量(训练集样本点和待分类点的输出变量)的方差。
下面对这个误分类损失进行更细节的论述。令 $k^*$ 为在 $x$ 点处得票最高的类别,并且 $p_k(x)$ 为类别 $k$ 的真实条件概率。那么:
$$\begin{align} \text{Bayes error} &= 1-p_{k^*}(x) \tag{13.2}\\ \text{1-nearest-neighbor error} &= \sum_{k=1}^K p_k(x)(1-p_k(x)) \tag{13.3}\\ &\geq 1-p_{k^*}(x) \tag{13.4} \end{align}$$1 最近邻的渐进误差率是一个随机规则的误差率,分类结果和测试样本点的选取都是随机的,服从的概率为 $p_k(x),k=1,\dots,K$。当 $K=2$ 时,1 最近邻误差率不大于二倍的贝叶斯错误率:
$$2 p_{k^*}(x)(1-p_{k^*}(x)) \leq 2(1-p_{k^*}(x))$$更一般地来说,可证明(练习 13.3):
$$\begin{align} & \sum_{k=1}^K p_k(x)(1-p_k(x)) \leq \\ & 2 (1-p_{k^*}(x)) - \frac{K}{K-1}(1-p_{k^*}(x))^2 \end{align}\tag{13.5}$$可推导出很多其他这种结果,可参考 Ripley (1996)。
这个结果可以为在某给定问题上可实现的最佳表现提供一个大致的概念。例如如果 1 最近邻分类规则的错误率为 10%,那么渐进条件下贝叶斯错误率至少为 5%。不过这里的一个关键是“渐进条件”,在这个假设下最近邻规则的偏差为零。在实际的问题中,偏差可能是不可忽视的。本章后续介绍的自适应最近邻分类规则就是在试图降低这个偏差。对于普通的最近邻模型,偏差和方差的特性可能决定了给定问题中的最优近邻数量。接下来的例子将说明这一点。
13.3.1 例:一个比较研究
我们在两个模拟问题中对最近邻、K 均值、和学习向量量化分类器进行测试。有 10 个独立的特征变量 $X_j$,都是 $[0,1]$ 上的均匀分布。两个类别的 0-1 目标变量定义如下:
$$\begin{align} & Y=I \left ( X_1 > \frac{1}{2} \right ) &\text{problem 1: "easy"} \\ & Y=I \left ( \operatorname{sign} \left \{ \prod_{j=1}^3(X_j-\frac{1}{2}) \right \} \right ) &\text{problem 2: "difficult"} \end{align}\tag{13.6}$$因此,第一个问题中的两个类别可被超平面 $X_1=1/2$ 分离;第二个问题中的两个类别在前三个特征定义的超立方体中形成了一个棋盘的样式。两个问题的贝叶斯错误率都为零。训练集大小为 100,测试集大小为 1000。
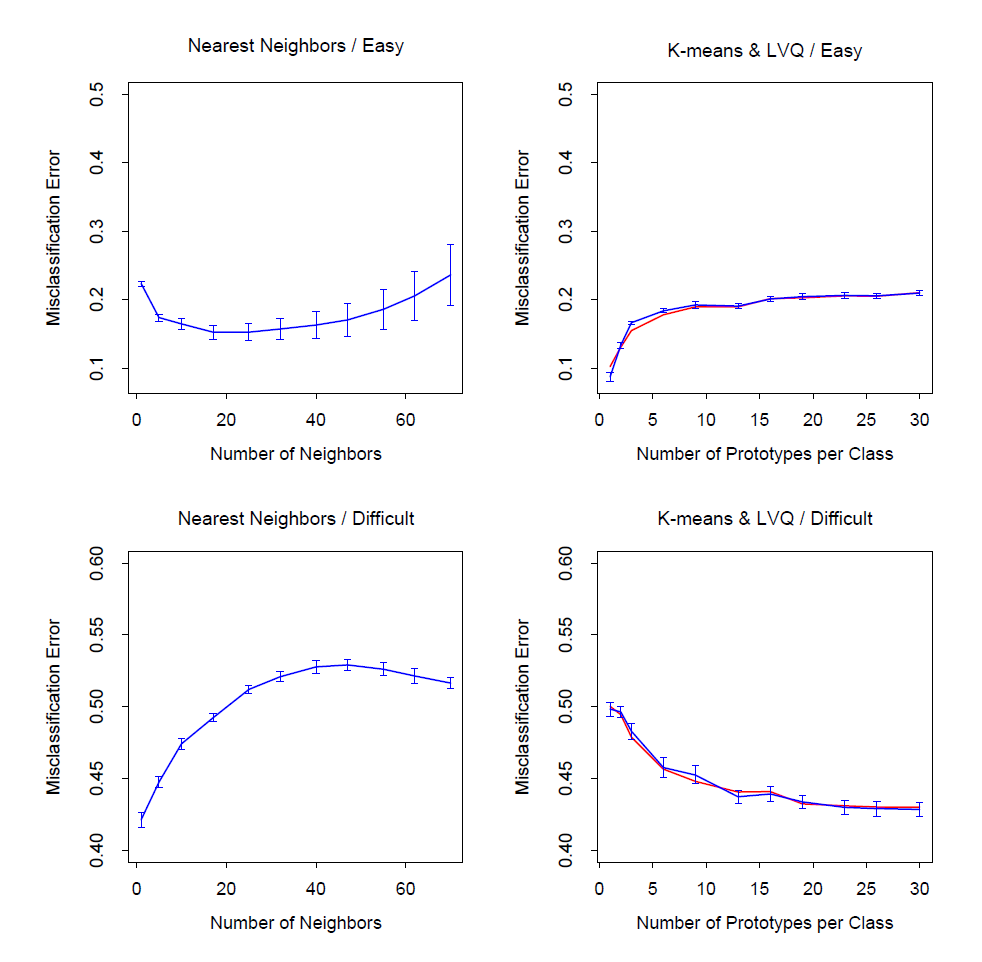
图 13.5展示了最近邻、K 均值、和学习向量量化(LVQ)的误分类误差率的均值和标准差,三个模型分别在不同的调整参数下实现了十次。可见 K 均值和 LVQ 得到了几乎一样的结果。在选择各自最优的调整参数条件下,K 均值和 LVQ 在第一个问题中表现优于最近邻,而它们在第二个问题中的表现相似。需要注意调整参数的最优取值显然是依赖于具体问题的。例如在第一个问题中,25 最近邻优于 1 最近邻,误差率降低到后者的 70%,而在第二个问题中,1 最近邻是最佳调整参数,误差率降低了 18%。1这些结果说明了使用例如交叉验证这种客观、数据驱动的方法来估计调整参数最优取值是非常重要的(参考图 13.4 和第七章)。
13.3.2 示例:k 最近邻和图片场景分类
STATLOG 项目(Michie et al., 1994)使用了 LANDSAT(陆地卫星)图片中的一部分($82\times100$ 像素)作为一个分类模型的基准问题。图 13.6展示了一片澳大利亚农业用地区域的热图(Heatmap),两个为可见光谱两个为红外光谱。每个像素点都有取值在 7 个元素集合 $\mathcal{G}=\{红土, 棉花, 种植茬, 混合, 灰土, 湿灰土, 特湿灰土\}$ 上的类别标签,这些标签由勘测这个区域的研究助理手动添加的。下中图展示了用不同颜色标记类别的实际土地用途。模型的目标是基于四个光谱图中的信息识别每个像素点的土地用途。
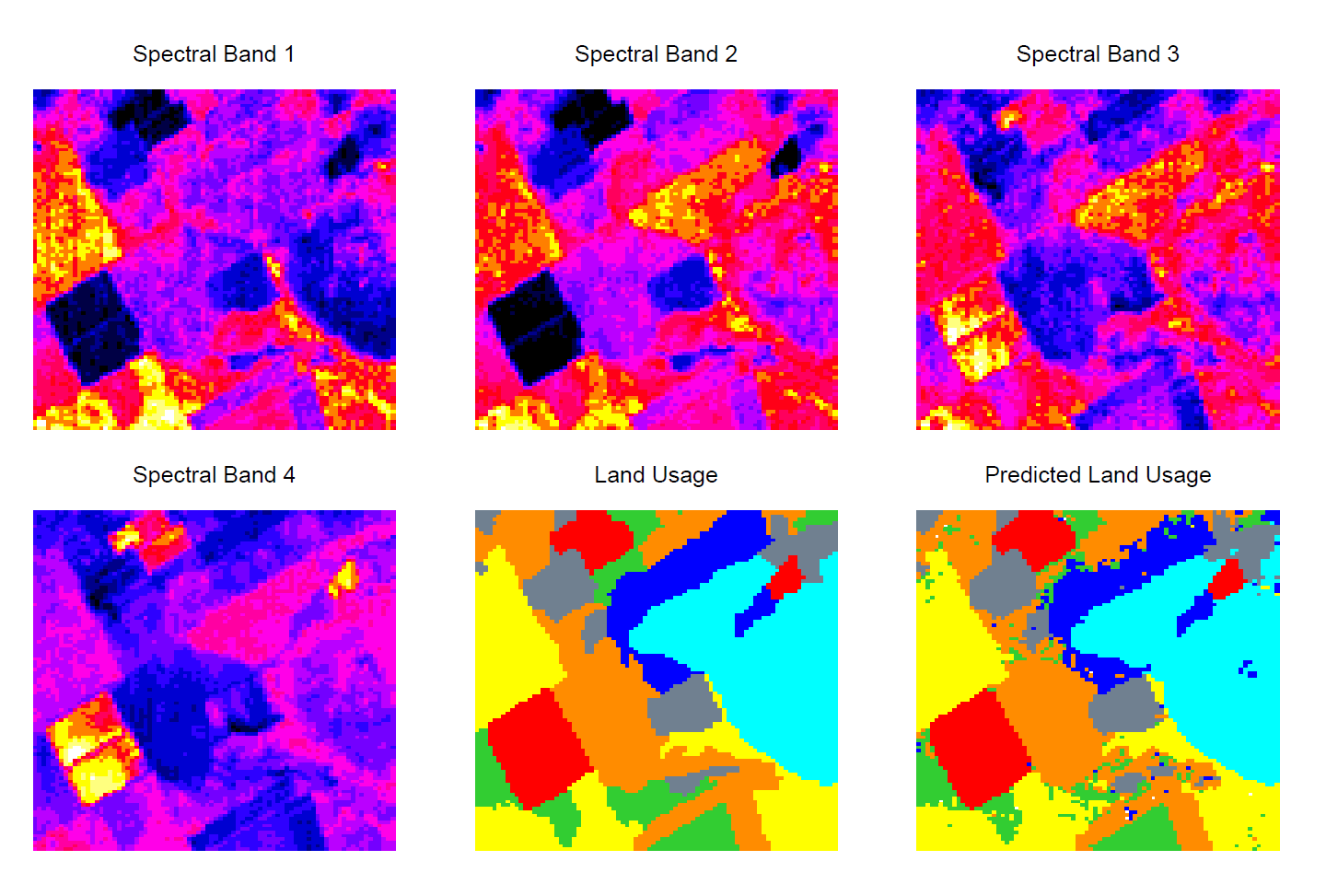
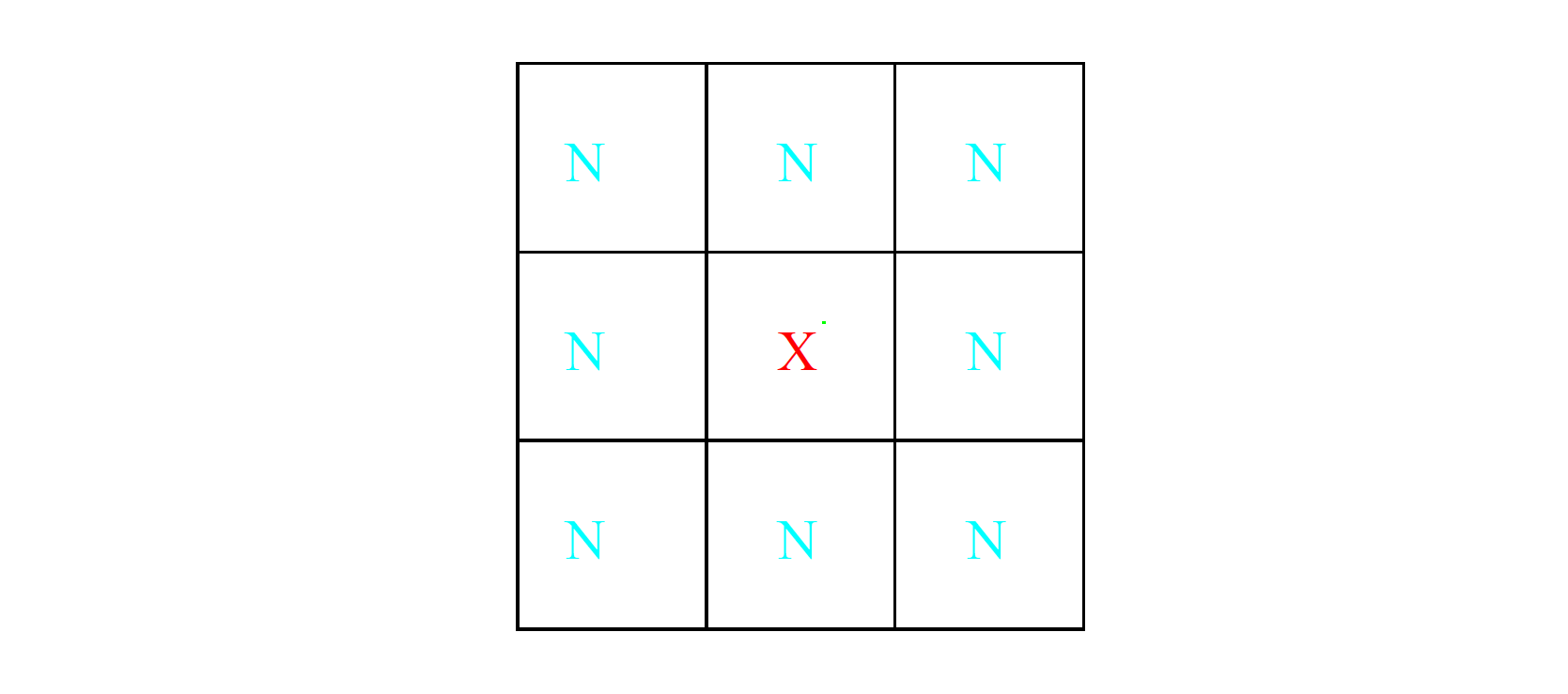
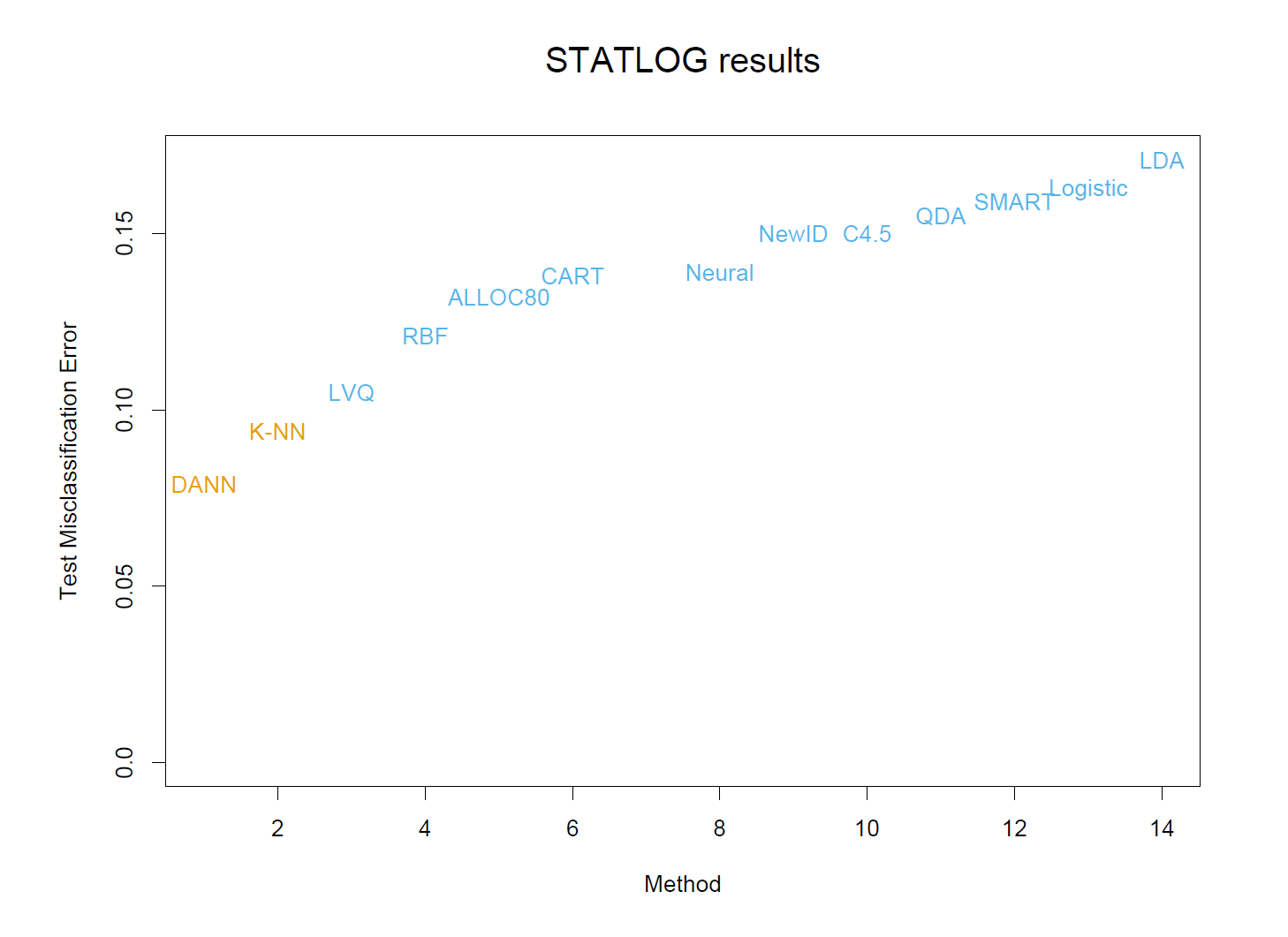
下右图展示了 5 最近邻得出的预测图,其计算过程如下。对每个像素点,我们抽取一个包含 8 个邻域点的特征图,即这个像素点以及其直接相邻的 8 个点(参考图 13.7)。在四个光谱图中分别进行这个操作,每个像素点便有 $(1+8)\times4=36$ 个输入特征变量。然后在这个 36 维的特征空间上使用 5 最近邻分类方法。最终的测试误差率大概为 9.5%(参考图 13.8)。在 STATLOG 项目使用的所有方法中,包含了 LVQ、CART、神经网络、线性判别分析、和很多其他的模型,在这个任务中 k 最近邻效果最好。可见在 $\mathbb{R}^{36}$ 上的决策边界可能是非常不规则的。
13.3.3 不变度量和切空间距离
在某些问题中,(同一类别)训练样本的特征在一些特定自然的转换后是不变的。最近邻分类器可以利用这个不变性,将它考虑在测量实例之间距离的度量定义中。这里用一个例子如何成功地运用这个思路,并得到了在当时最佳的分类效果(Simard et al., 1993)。
考虑手写数字识别的问题,它在第一章和第 11.7 节都已有介绍。输入变量是 $16\times16=256$ 个像素点的灰度图片,图 13.9 给出了一些示例。图 13.10 的上部展示了数字“3”,包括它实际的方向(正中)以及向两个方向旋转 7.5° 和 15°。在真实的手写数字中这种旋转会经常出现,用肉眼可很容易分辨即使有小的旋转“3”也仍然是“3”。所以我们需要让最近邻分类器将这些“3”认定为互相接近/相似。不过旋转“3”的 256 个灰度像素值可能与原始图的值非常不同,因此这两者在 $\mathbb{R}^{256}$ 空间上的欧式距离可能非常远。

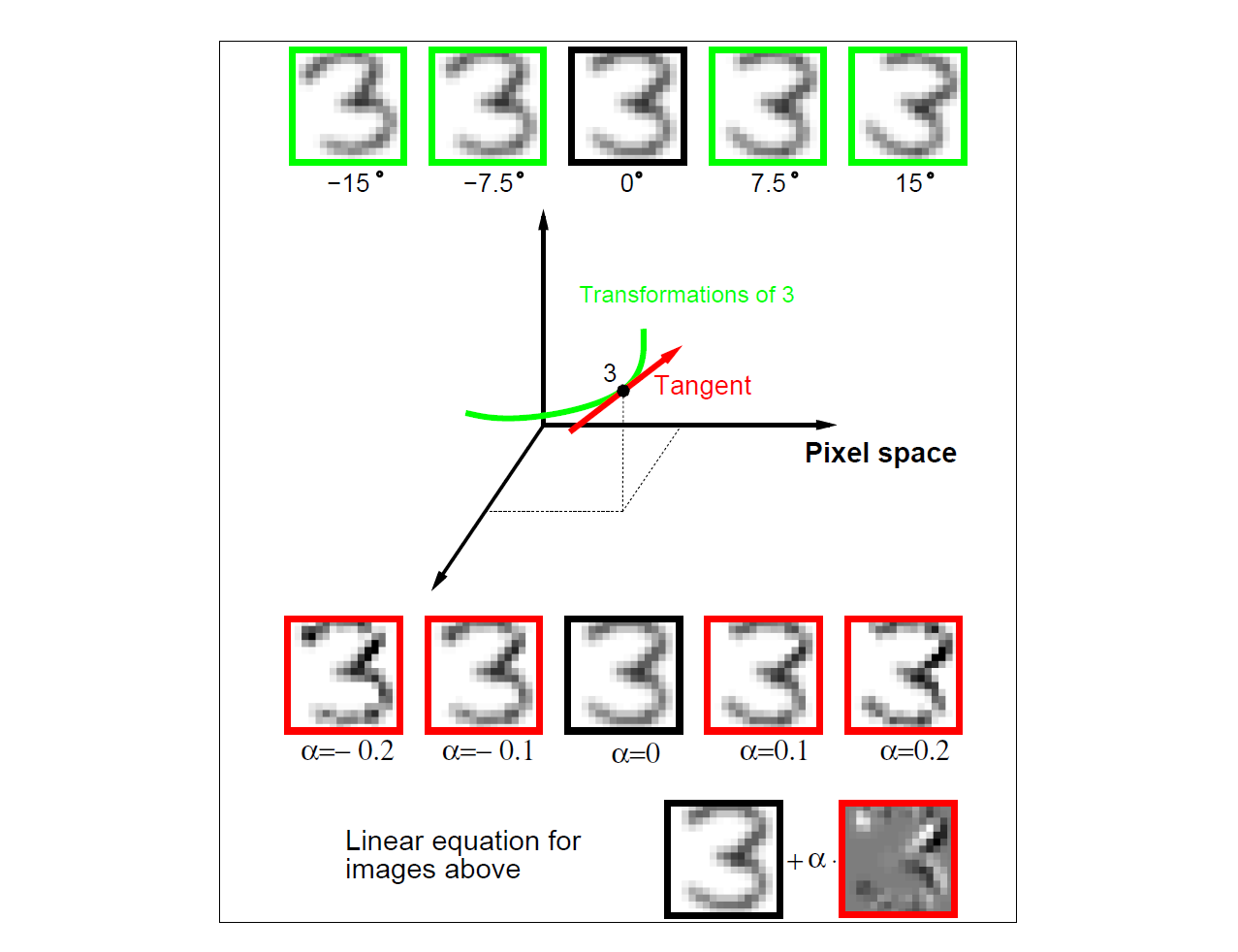
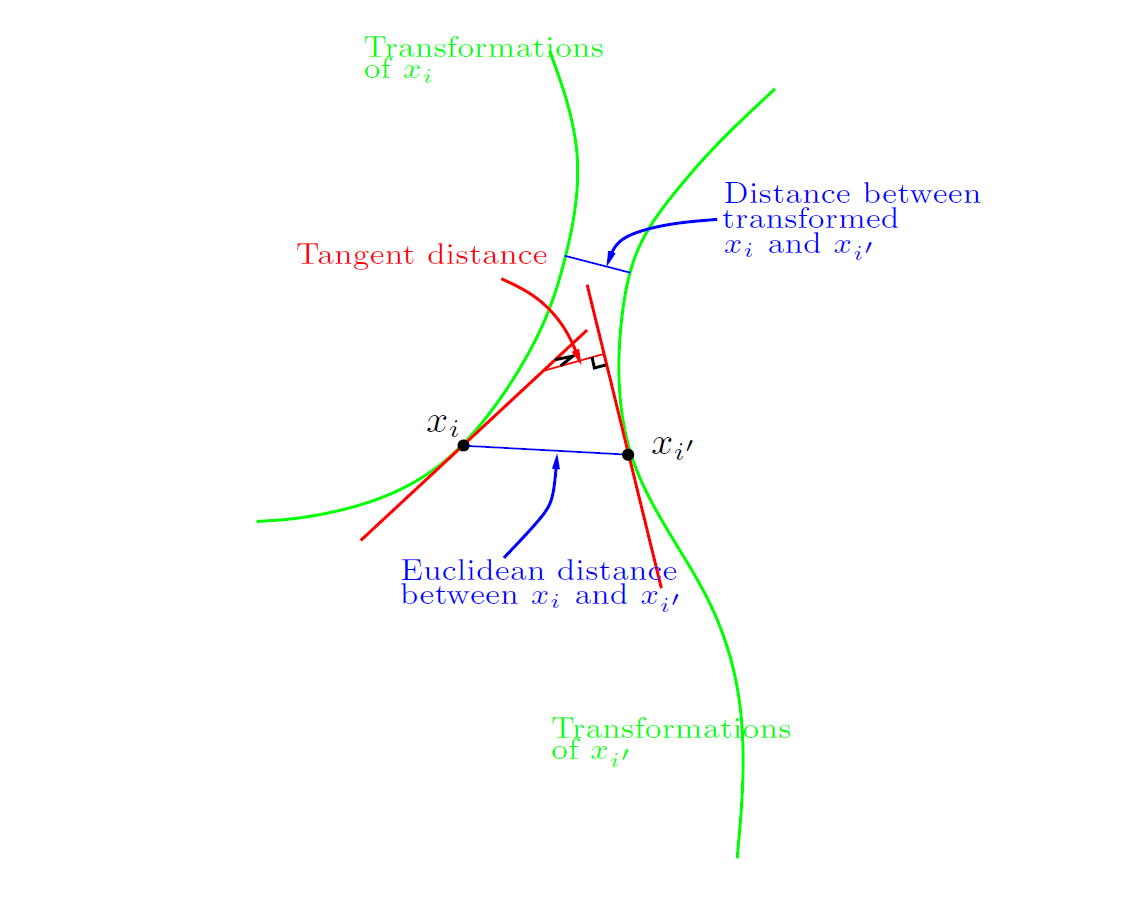
我们想要在测量同一类别中的两个数字图片之间的距离时旋转所带来的影响。考虑原始的“3”和它旋转版本的一系列像素值。可以将它想象为在 $\mathbb{R}^256$ 空间上的一维曲线,即图 13.10 中所表现的穿过“3”标记的点的绿色曲线。图 13.11 是一个表现 $\mathbb{R}^{256}$ 空间的(非实际)示意图,两个图片标记为 $x_i$ 和 $x_{i’}$。它们可能就是两个不同的“3”。两个图片各有一个代表了其旋转版本的曲线穿过这个图片,在这里被称为 不变流形(invariance manifold)。这样我们就不再使用两个图片之间常规的欧式距离了,而使用两条曲线之间最短的距离。也就是说两个图片之间的距离被定义为第一个图片的任意旋转版本与第二个图片的任意旋转版本之间的最小欧式距离。这个距离被称之为 不变度量(invariant metric)。
理论上来说可以在 1 最近邻分类模型中使用这个不变度量。但是这会存在两个问题。首先,在真实图片上的计算会非常困难。其次,它会引入大幅度的转换从而导致分类表现不佳。例如,数字“6”在经过 180° 的转换后可能会被认定接近于“9”。我们需要将模型约束在小幅度的旋转中。
使用 切空间距离(tangent distance) 可以解决上述的两个问题。如图 13.10 中所见,我们可以用在原始图片处的切线来概括这个图片“3”的不变流形。这个切线的计算可以通过对这个图片微小旋转的方向向量的估计,或者通过更复杂的空间平滑方法(练习 13.4)。大幅度旋转后的图片,其切线上的图片不再与“3”相似,因此就缓解了大幅度转换带来的问题。
之后的思路就是去计算每个样本图片的不变切线。给定了一个待分类图片,我们需要计算它的不变切线,然后在训练集的切线中寻找与其距离最近的切线。这个距离最近切线所对应的类别(数字)即为(1 最近邻)模型对图片的预测分类。图 13.11 中两个切线相交了,不过这只是因为我们只能为 256 维的实际空间做一个二维的示意图。在 $\mathbb{R}^{256}$ 空间上,像这样的两个切线相交的可能性基本为零。
要实现这种不变性,另一个更简单的方式是在训练集中为每个训练图片添加一些旋转过的图片,然后只需要使用一个普通的最近邻分类器。这个思路在 Abu-Mostafa (1995) 中被称为“提示(hints)”,而且当不变性的空间较小时比较有效。目前我们只展示出了这个问题的一个简化的版本。除了旋转之外还有其他六种类型的转换,我们希望分类器可以对它们都有不变性。包括了两个方向的平移(translation)、两个方向的缩放(scaling)、偏向扭曲(sheer)、和笔画粗细(thickness)。因此图 13.10 和图 13.11 中的曲线和切线实际上是 7 个维度的流形或超平面。为每个训练图片添加可以捕捉所有这些可能转换的新样本是不可行的。切线流形则为实现这些不变性提供了一个简洁的方法。
表 13.1 展示了这个问题的测试误分类误差率,数据中有 7291 个训练图片和 2007 各测试图片(美国邮政服务数据集),模型包括一个特意构建的神经网络、普通的 1 最近邻、和使用切空间距离的 1 最近邻。切空间距离最近邻分类器的表现非常好,其测试误差率接近于肉眼识别的误差率。(而这是一个总所周知难以处理的测试集)。然而在实践中,最近邻的速度太慢不适合应用于在线的分类(参考第 13.5 节),并且神经网络分类器随后也发展出与之相似的效果了。
| 方法 | Error rate |
|---|---|
| Neural-net | 0.049 |
| 1-nearest-neighbor/Euclidean distance | 0.055 |
| 1-nearest-neighbor/tangent distance | 0.026 |
表 13.1:手写邮编识别问题中的测试误差率。
本节练习
练习 13.3
Let E∗ be the error rate of the Bayes rule in a K-class problem, where the true class probabilities are given by pk(x), k = 1,…,K. Assuming the test point and training point have identical features x, prove (13.5)
$$\sum_{k=1}^K p_k(x)(1-p_k(x)) \leq 2(1-p_{k^*}(x)) - \frac{K}{K-1}(1-p_{k^*}(x))^2$$where k∗ = argmaxkpk(x). Hence argue that the error rate of the 1nearest-neighbor rule converges in L1, as the size of the training set increases, to a value E1, bounded above by
$$\operatorname{E}^* \left ( 2 - \operatorname{E}^*\frac{K}{K-1} \right ) \tag{13.12}$$[This statement of the theorem of Cover and Hart (1967) is taken from Chapter 6 of Ripley (1996), where a short proof is also given].
练习 13.4
-
译者从原文并没有确定这两个百分比(70% 和 18%)的含义,这里是从图中猜测的。 ↩︎