线性判别分析也可被理解为是一种原型(prototype)分类器。每个类别可由它的中心点所代表,而分类规则就是按一个恰当度量距离最近的中心点的类别。很多时候一个原型并不足以代表不均一的类别,而混合模型就会更合理。本节我们回顾高斯混合(Gaussian mixture)模型,并说明它们可以通过上面介绍的 FDA 和 PDA 方法进行扩展。类别 $k$ 的高斯混合模型密度函数为
$$P(X|G=k) = \sum_{r=1}^{R_k} \pi_{kr} \phi(X; \mu_{kr}, \mathbf{\Sigma}) \tag{12.59}$$其中的混合比例 $\pi_{kr}$ 和为一。这个模型中第 $k$ 类别有 $R_k$ 个原型,而且在这里所有密度函数中都使用了同一个协方差矩阵 $\mathbf{\Sigma}$。每个类别给定了这样的概率模型后,类别的后验概率则为
$$P(G=k|X=x) = \frac {\sum_{r=1}^{R_k} \pi_{kr} \phi(X;\mu_{kr},\mathbf{\Sigma}) \Pi_k} {\sum_{\ell=1}^K \sum_{r=1}^{R_\ell} \pi_{\ell r} \phi(X;\mu_{\ell r},\mathbf{\Sigma}) \Pi_\ell} \tag{12.60}$$其中的 $\Pi_k$ 代表了类别的先验概率。
在第八章中介绍了两个成分特例的计算过程。与 LDA 类似地,我们用最大似然方法估计参数,而基于 $P(G,X)$ 的联合对数似然函数为:
$$\sum_{k=1}^K \sum_{g_i=k} \log \left[ \sum_{r=1}^{R_k} \pi_{kr} \phi(x_i;\mu_{kr},\mathbf{\Sigma}) \Pi_k \right] \tag{12.61}$$若直接计算,log 函数中的求和会使最优化问题异常繁杂。计算混合分布模型的最大似然估计(MLE)经典常用的方法是 EM 算法(Dempster et al., 1977),已知这个算法具备良好的收敛性质。EM 算法交替进行以下两步:
- 期望(E)步骤:基于当前的参数值,为类别 $k$ 中的每个样本($g_i=k$)计算子类别 $c_{kr}$ 的“责任值(responsibility)”。 $$W(c_{kr}|x_i,g_i) = \frac {\pi_{kr}\phi(x_i;\mu_{kr},\mathbf{\Sigma})} {\sum_{\ell=1}^{R_k} \pi_{k\ell}\phi(x_i;\mu_{k\ell},\mathbf{\Sigma})} \tag{12.62}$$
- 最大化(M)步骤:使用 E 步骤中的权重,为每个类别中的每个高斯成分的参数计算加权最大似然估计。
在 E 步骤中,算法将类别 $K$ 中的一个样本的单位权重分派给这个类别的多个子类别。如果这个样本点与某个子类别中心点很近而距离其他的很远,那么这个子类别的权重会接近于一。另一方面,如果样本点位于两个子类别中间的位置,那么两个子类别会得到相同的权重。
在 M 步骤中,类别 $k$ 中的一个样本会被用于所有 $R_k$ 个成分密度参数的估计,也就是会被使用 $R_k$ 次,每次的权重不一样。第八章中介绍了 EM 算法的细节。算法需要选取初始化参数,而由于混合模型的似然函数一般是多峰的(multimodal),初始参数可能对结果有影响。我们使用的软件(计算量考量中会提到)提供了不同的处理策略,这里介绍下默认的方案。首先为每个类别指定子类别的个数 $R_k$。在类别 $k$ 的样本上,使用多个随机的初始化参数拟合 K 均值聚类模型。这样将样本点分配到了 $R_k$ 个不相交的集合中,据此就可得到一个初始化的由零和一组成的权重矩阵。
各成分协方差矩阵 $\mathbf{\Sigma}$ 相同的假设,可以使我们进一步地简化。与 LDA 类似,可以在混合模型的公式中对秩进行约束。为说明这一点,我们回顾关于 LDA 的一个已知的结论。$L$ 秩的 LDA 拟合(第 4.3.3 节),与每个类别的均值向量被约束在 $\mathbb{R}^p$ 的 $L$ 维子空间上的高斯分布模型的最大似然拟合,是等价的(练习 4.8)。混合模型也有这个性质,所以可以在所有 $\sum_k R_k$ 个中心点的秩约束 $\operatorname{rank}\{\mu_{k\ell}\}=L$ 下进行对数似然函数 12.61 的最大化。
这是仍可以使用 EM 算法,M 步骤就成为了一个加权版本的 LDA,其“类别”个数为 $R=\sum_{k=1}^K R_k$。此外,在解这个加权 LDA 问题时,也可以和之前一样使用最优评分函数,这样这一步就是在进行一个加权版本的 FDA 或者 PDA。除了“类别”的个数会增加外,可能会觉得在类别 $k$ 中“样本”的数量也会按 $R_k$ 的比例增加。当最优评分回归中使用的是线性运算的情况下,事实并不如此。在这个情况下,扩大的指示矩阵 $\mathbf{Y}$ 缩减为一个模糊输出变量矩阵 $\mathbf{Z}$,从直观理解这是有利的。例如,如果有 $K=3$ 个类别,每个类别有 $R_k=3$ 个子类别,那么 $\mathbf{Z}$ 可能看起来是这样:
$$\begin{matrix} & \begin{matrix} c_{11}&c_{12}&c_{13}&c_{21}&c_{22}&c_{23}&c_{31}&c_{32}&c_{33} \end{matrix} \\ \begin{matrix}g_1=2\\g_2=1\\g_3=1\\g_4=3\\g_5=2\\\vdots\\g_N=3\end{matrix} & \begin{pmatrix} 0 & 0 & 0 & 0.3 & 0.5 & 0.2 & 0 & 0 & 0 \\ 0.9 & 0.1 & 0.0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0.1 & 0.8 & 0.1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0.5 & 0.4 & 0.1 \\ 0 & 0 & 0 & 0.7 & 0.1 & 0.2 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & 0 & 0.1 & 0.1 & 0.8 \\ \end{pmatrix} \end{matrix}$$ $$\tag{12.63}$$其中某个类别 $k$ 行的元素对应的是 $W(c_{kr}|x,g_i)$。
之后的步骤是一样的:
$$\text{M-step of MDA } \begin{cases} \hat{\mathbf{Z}} = \mathbf{S}\mathbf{Z} \\ \mathbf{Z}^T\hat{\mathbf{Z}} = \mathbf{\Theta}\mathbf{D}\mathbf{\Theta}^T \\ \text{更新这些 }\pi\text{ 和 }\Pi \end{cases}$$这些简单改动给混合模型带来了很大的灵活性:
- 在 LDA、FDA、或 PDA 中,维度缩减的步骤受限于类别的个数。特别来说,当只有 $K=2$ 个类别时就无法进行缩减。而 MDA 用子类别代替了类别,然后就可以在这些子类别中心点组成的子空间上观察其低维度的视图。这个子空间通常会是判别中的重要的子空间。
- M 步骤中使用 FDA 或 PDA,可以使我们采用更适合具体场景的方法。例如我们就可以在模拟信号和图片的 MDA 拟合中加入平滑约束。
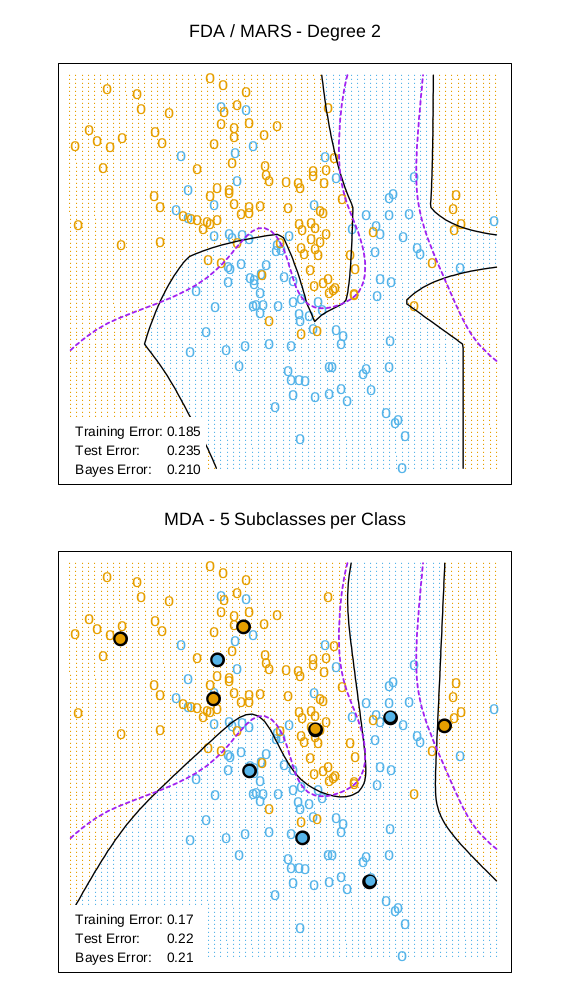
图 12.13 在混合分布的例子中比较了 FDA 和 MDA。
12.7.1 示例:波形数据
本节用一个常用的模拟例子来演示这些方法,这个例子来自 Breiman et al. (1984, p 49-55),也在 Hastie and Tibshirani (1996b) 和其他文献中被使用过。这是一个有 21 个自变量和三个类别的分类问题,并且被认为是一个较难处理的模式识别问题。自变量的定义为:
$$\begin{align} X_j &= U h_1(j) + (1-U) h_2(j) + \epsilon_j & \text{类别 1} \\ X_j &= U h_1(j) + (1-U) h_3(j) + \epsilon_j & \text{类别 2} \\ X_j &= U h_2(j) + (1-U) h_3(j) + \epsilon_j & \text{类别 3} \end{align}\tag{12.64}$$其中 $j=1,2,\dots,21$,$U$ 为 $(0,1)$ 上的均匀分布,$\epsilon_j$ 为标准正态分布,$h_\ell$ 为有带平移的三角波形函数:
- $h_1(j)=\max(6-|j-11|)$
- $h_2(j)=h_1(j-4)$
- $h_3(j)=h_1(j+4)$
图 12.14 展示了每个类别中的一些波形函数示例。

表 12.4 展示了应用在波形数据上的 MDA 以及本章和其他章节中一些方法的表现结果。训练集有 300 个观测样本,并且使用了等分的先验概率,即每个类型大概有 100 个观测样本。测试集的大小为 500。表的说明中描述了其中的两个 MDA 模型。
| Error Rates | Error Rates | |
|---|---|---|
| Technique | Training | Test |
| LDA | 0.121(0.006) | 0.191(0.006) |
| QDA | 0.039(0.004) | 0.205(0.006) |
| CART | 0.072(0.003) | 0.289(0.004) |
| FDA/MARS (degree = 1) | 0.100(0.006) | 0.191(0.006) |
| FDA/MARS (degree = 2) | 0.068(0.004) | 0.215(0.002) |
| MDA (3 subclasses) | 0.087(0.005) | 0.169(0.006) |
| MDA (3 subclasses, penalized 4 df) | 0.137(0.006) | 0.157(0.005) |
| PDA (penalized 4 df) | 0.150(0.005) | 0.171(0.005) |
| Bayes | 0.140 |
表 12.4:波形数据的结果。数值为十次模拟的平均值,括号内为平均值的标准差。前五行结果来自 Hastie et al. (1994)。第六行的模型为每个类别三个子类别的 MDA。第七行的模型一样,不过通过等同于 4 个自由度的粗糙度惩罚项对判别系数进行了惩罚。第八行为对应的惩罚 LDA 或者是 PDA 模型。

图 12.15展示了带惩罚 MDA 在测试集上计算的主要典型变量。可能已经猜到,类别似乎位于一个三角形的边上。这是因为 $h_j(i)$ 被 21 维空间上的三个点所代表,从而形成了三角形的顶点;每个类别是一对顶点的凸性组合,因此位于一个边上。并且可看出所有的有用信息都出现在前两个维度中;前两个坐标可解释 99.8% 比例的方差。将模型解截断在这里对结果没有任何影响。这个问题的贝叶斯风险(错误率)估计为大约 0.14(Breiman et al., 1984)。MDA 结果接近最优错误率;这也是合理的,因为这个数据的生成模型与 MDA 模型的结构是相似的。