变量子集选择方法对进入模型的自变量进行筛选,从而增强了模型的可解释性,并且其预测误差可能比完整模型更小。然而由于选择过程是离散的,即某个变量或者被模型使用或者被排除,它的方差通常比较高所以并没有降低完整模型的预测误差。收缩方法的做法更“连续”,从而不会有类似增减一个自变量的较大变动。
3.4.1 岭回归
岭回归(Ridge regression) 通过对回归系数的大小进行惩罚,从而对回归系数进行了收缩(shrink)。岭回归的最小化目标函数是一个带惩罚项的残常平方和:
$$\hat{\beta}^{\text{ridge}} = \underset{\beta}{\arg\min} \left\{ \sum_{i=1}^N (y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 + \lambda \sum_{j=1}^p \beta_j^2 \right\}\tag{3.41}$$其中的 $\lambda\geq0$ 是一个控制收缩程度的复杂度参数:$\lambda$ 的值越大,收缩的程度越大。最小化得到的系数会向 0 点的方向收缩(同时与彼此之间的距离也更近)。神经网络中也会使用这种参数平方和的惩罚,称之为 权值衰减(weight decay)(第十一章)。
岭回归也可等价地写为:
$$\begin{align} \hat{\beta}^{\text{ridge}} &= \underset{\beta}{\arg\min} \sum_{i=1}^N (y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 \\ & \text{subject to } \sum_{j=1}^p \beta_j^2 \leq t \end{align}\tag{3.42}$$这里对参数的大小进行了显式的限制。定义 3.41 中的参数 $\lambda$ 与定义 3.42 中的参数 $t$ 存在着一一对应的转换关系。当线性回归模型中存在很多互相相关的输入变量时,它们的系数估计可能非常不准确,且方差很大。直观上来说,若两个输入变量相关性很强,则两个系数可同时估计为绝对值很大的正负两个估计,却可以互相抵消而对整体的拟合影响不大。岭回归通过对系数整体大小的限制,可缓解这样的问题。
岭回归的解会被输入变量的缩放尺度所影响1,所以通常的做法是在求解 3.41 中的最小化之前,先对输入变量进行标准化。另外,需要注意惩罚项中不包含截距项 $\beta_0$。如果在惩罚项中加入截距,会使模型的结果依赖于输出变量 $Y$ 的度量原点;如果将所有的输出变量 $y_i$ 加上同样的常数 $c$,预测结果不会同样地增加常数 $c$。可证明(练习 3.5),使用中心化的输入变量后,最小化问题 3.41 的解可以分成两部分:对输入变量的中心化,即用 $x_{ij}-\bar{x}_j$ 代替 $x_{ij}$;截距项 $\beta_0$ 的估计值为输出变量的样本均值 $\bar{y}=\frac{1}{N}\sum_{i=1}^Ny_i$;其他的系数则使用无截距项、中心化的输入变量的岭回归来估计。下文中我们会假设输入变量和输出变量均已经过中心化处理,故输入变量矩阵 $\mathbf{X}$ 的列数为 $p$ 而不是 $p+1$。
将式 3.41 的最小化目标函数用矩阵形式表达:
$$\operatorname{RSS}(\lambda) = (\mathbf{y}-\mathbf{X}\beta)^T(\mathbf{y}-\mathbf{X}\beta) + \lambda \beta^T\beta \tag{3.43}$$则可通过矩阵求导获得岭回归的解:
$$\hat{\beta}^{\text{ridge}} = (\mathbf{X}^T\mathbf{X} + \lambda\mathbf{I})^{-1} \mathbf{X}\mathbf{y} \tag{3.44}$$其中 $\mathbf{I}$ 为 $p\times p$ 的单位矩阵。由于惩罚项是系数的二次形式 $\beta^T\beta$,岭回归的解仍是 $\mathbf{y}$ 的线性转换。(与最小二乘相比)这个解在取逆矩阵之前,在 $\mathbf{X}^T\mathbf{X}$ 的对角线元素上加上了一个正数。这样即使 $\mathbf{X}^T\mathbf{X}$ 为非满秩矩阵,这个矩阵求逆运算仍然是可行的。这实际上是统计学中引入岭回归的主要原因(Hoerl and Kennard, 1970)。因此,传统上直接通过等式 3.44 来定义岭回归。为了更清晰地了解其工作原理,本书中通过最小化问题的定义 3.41 和 3.42 来引入岭回归,

图 3.8 为前列腺癌症数据集上的岭回归系数的估计值,横轴为依赖于惩罚参数 $\lambda$ 的有效自由度 $\operatorname{df}(\lambda)$(定义见等式 3.50,effective degrees of freedom)。当输入变量为标准正交时,岭回归的系数估计是最小二乘的系数估计的线性收缩,即 $\hat{\beta}^{\text{ridge}}=\hat{\beta}/(1+\lambda)$。
选择一个恰当的先验分布后,岭回归的结果也可理解为后验分布的均值或者众数。假设 $y_i\sim\mathcal{N}(\beta_0+x^T_i\beta,\sigma^2)$,每个参数 $\beta_j$ 都服从分布 $\mathcal{N}(0,\tau^2)$,并相互独立。则在 $\tau^2$ 和 $\sigma^2$ 已知的假设下,$\beta$ 的(负)对数后验密度函数等同于式 3.41 中花括号包围的部分,并且 $\lambda=\sigma^2/\tau^2$(练习 3.6)。因此,岭回归的系数估计,也就是这个后验分布的众数或均值(高斯分布的众数与均值相同)。
中心化输入变量矩阵 $\mathbf{X}$ 的 奇异值分解(singular value decomposition, SVD) 可帮助我们从另一个角度来理解岭回归的本质。这个矩阵分解在很多统计学方法中都很有用。一个维度为 $N\times p$ 的矩阵 $\mathbf{X}$ 的奇异值分解为2:
$$\mathbf{X} = \mathbf{U}\mathbf{D}\mathbf{V}^T \tag{3.45}$$其中 $\mathbf{U}$ 和 $\mathbf{V}$ 分别为 $N\times p$ 和 $p\times p$ 的正交矩阵。矩阵 $\mathbf{U}$ 的列张成(span)矩阵 $\mathbf{X}$ 的列空间;矩阵 $\mathbf{V}$ 的列张成矩阵 $\mathbf{X}$ 的行空间。矩阵 $\mathbf{D}$ 为 $p\times p$ 的对角矩阵,对角线元素 $d_1\geq d_2\geq\dots\geq d_p\geq0$ 称为 $\mathbf{X}$ 的奇异值。如果任意一个 $d_j=0$,则 $\mathbf{X}$ 为奇异矩阵。
利用奇异值分解,可以将最小二乘的输出变量拟合值向量化简为:
$$\begin{align} \mathbf{X}\hat{\beta}^{\text{ls}} &= \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} \\ &= \mathbf{U}\mathbf{U}^T\mathbf{y}\tag{3.46} \end{align}$$式 3.46 的推导
参考 Weatherwax and Epstein (2021) page 24。
$$\begin{align}\mathbf{X}^T\mathbf{X} &= (\mathbf{U}\mathbf{D}\mathbf{V}^T)^T\mathbf{U}\mathbf{D}\mathbf{V}^T = \mathbf{V}\mathbf{D}\mathbf{U}^T\mathbf{U}\mathbf{D}\mathbf{V}^T \\ &= \mathbf{V}\mathbf{D}\mathbf{I}_p\mathbf{D}\mathbf{V}^T = \mathbf{V}\mathbf{D}^2\mathbf{V}^T \end{align}$$
将其带入到式 3.46,并使用逆矩阵的性质:
$$\begin{align} \mathbf{X}\hat{\beta}^{\text{ls}} &= \mathbf{U}\mathbf{D}\mathbf{V}^T(\mathbf{V}^T)^{-1}(\mathbf{D}^{-1})^2\mathbf{V}^{-1}\mathbf{V}\mathbf{D}\mathbf{U}^T\mathbf{y} \\ &= \mathbf{U}\mathbf{D}(\mathbf{D}^{-1})^2\mathbf{D}\mathbf{U}^T\mathbf{y} \\ &= \mathbf{U}\mathbf{U}^T\mathbf{y} \end{align}$$
其中的 $\mathbf{U}^T\mathbf{y}$ 就是 $\mathbf{y}$ 在标准正交基 $\mathbf{U}$ 上的坐标。另外可见上式与等式 3.33 十分相似,$\mathbf{Q}$ 和 $\mathbf{U}$ 一般来说是对矩阵 $\mathbf{X}$ 列空间的两组不同的正交基(练习 3.8)。
式 3.33
$$\hat{\mathbf{y}} = \mathbf{Q}\mathbf{Q}^T\mathbf{y}\tag{3.33}$$
$\mathbf{Q}$ 为 $\mathbf{X}$ 的 QR 分解中的 Q 正交矩阵。
利用奇异值分解,岭回归的拟合可写为:
$$\begin{align} \mathbf{X}\hat{\beta}^{\text{ridge}} &= \mathbf{X}(\mathbf{X}^T\mathbf{X}+\lambda\mathbf{I})^{-1} \mathbf{X}^T\mathbf{y} \\ &= \mathbf{U}\mathbf{D}(\mathbf{D}^2+\lambda\mathbf{I})^{-1} \mathbf{D}\mathbf{U}^T\mathbf{y} \\ &= \sum_{j=1}^p \mathbf{u}_j \frac{d_j^2}{d_j^2+\lambda} \mathbf{u}^T \mathbf{y} \tag{3.47}\end{align}$$其中的 $\mathbf{u}_j$ 为 $\mathbf{U}$ 的列向量。由于 $\lambda\geq 0$,中间的分数 $d_j^2/(d_j^2+\lambda)\leq1$。与最小二乘类似,岭回归的拟合同样是计算 $\mathbf{y}$ 在标准正交基 $\mathbf{U}$ 上的坐标。但之后它将这些坐标以因子 $d_j^2/(d_j^2+\lambda)$ 进行收缩。所以 $d_j^2$ 越小,其相应的基向量的坐标的收缩程度越大。
当 $d_j^2$ 的值比较小时意味着什么?中心化的输入变量矩阵 $\mathbf{X}$ 的奇异值分解可看作是 $\mathbf{X}$ 中变量的 主成分(principal components) 的另一种表达方式。样本协方差矩阵为 $\mathbf{S}=\mathbf{X}^T\mathbf{X}/N$,从式 3.45 可得:
$$\mathbf{X}^T\mathbf{X} = \mathbf{V}\mathbf{D}^2\mathbf{V}^T\tag{3.48}$$这正是矩阵 $\mathbf{X}^T\mathbf{X}$(乘以 N 后的 $\mathbf{S}$)的 特征分解(eigen decomposition)。特征向量 $v_j$ (矩阵 $\mathbf{V}$ 的列向量)也被称为 $\mathbf{X}$ 的主成分方向,或 K-L(Karhunen-Loève)转换。第一个主成分方向 $v_1$ 使得 $\mathbf{z}_1=\mathbf{X}v_1$ 是所有 $\mathbf{X}$ 列向量的归一化线性组合中样本方差最大的。其样本方差为:
$$\operatorname{Var}(\mathbf{z}_1) = \operatorname{Var}(\mathbf{X}v_1) = \frac{d_1^2}{N} \tag{3.49}$$并且有 $\mathbf{z}_1=\mathbf{X}v_1=\mathbf{u}_1d_1$。这个衍生变量 $\mathbf{z}_1$ 即为 $\mathbf{X}$ 的第一主成分,而 $\mathbf{u}_1$ 即为归一化的第一主成分。后继的主成分 $\mathbf{z}_j$,为与所有先前的主成分正交并方差最大的线性组合,其样本方差为 $d_j^2/N$。最后一个主成分的样本方差最小,所以 $d_j$ 的值小对应着 $\mathbf{X}$ 的列空间中样本方差小的方向,岭回归在这些方向上的收缩程度更大。

图 3.9 以一些二维空间上的数据点演示主成分。假设这是一个二维的输入变量空间,输出变量的 Y 轴为垂直与屏幕/书页的方向,我们试图建立定义域为这个二维平面的线性平面。图中的输入变量样本的分布形状使得沿着长线方向要比短线方向的梯度计算更准确。岭回归避免在短线方向梯度估计时可能产生的大方差。这里隐含了一个假设:输出变量在样本方差大的方向上的变化更大。通常这个假设是合理的,实际场景中大多会选择研究与输出变量相关的输入变量,当然也必然会有例外的情况。
图 3.7
图 3.7 在第 3.3 节。

在上一节的图 3.7 中,预测误差估计的曲线为下式中定义的值的函数:
$$\begin{align} \operatorname{df}(\lambda) &= \operatorname{tr}[\mathbf{X}(\mathbf{X}^T\mathbf{X}+\lambda\mathbf{I})^{-1} \mathbf{X}^T] \\ &= \operatorname{tr}(\mathbf{H}\_{\lambda}) \\ &= \sum_{j=1}^p \frac{d_j^2}{d_j^2+\lambda} \tag{3.50} \end{align}$$这个对 $\lambda$ 单调递减的函数即为岭回归拟合的 有效自由度(effective degrees of freedom)。通常 $p$ 个变量的线性回归拟合的自由度,为其中的自由变动的参数的个数 $p$。在岭回归中,尽管全部 $p$ 个系数的估计值都不为 0,但拟合的过程是有限制的,限制的程度由 $\lambda$ 来控制。当 $\lambda=0$ 时,即没有正则项,$\operatorname{df}(\lambda)=p$;当 $\lambda\rightarrow\infty$ 时,$\operatorname{df}(\lambda)\rightarrow\infty$。当然如果回归中有截距项,则会增加一个自由度,在本节开始时已默认将所有变量中心化,去除了截距。第 3.4.4 和 7.4-7.6 节会更深入地理解自由度的概念。在图 3.7 中,最终选取的岭回归(右上)自由度为 $\operatorname{df}(\lambda)=5.0$。在表 3.3 中,可以看到岭回归的测试误差比使用全部变量的最小二乘估计有一些降低。
| Term | LS | Best Subset | Ridge | Lasso | PCR | PLS |
|---|---|---|---|---|---|---|
| Intercept | 2.465 | 2.477 | 2.452 | 2.468 | 2.497 | 2.452 |
| lcavol | 0.680 | 0.740 | 0.420 | 0.533 | 0.543 | 0.419 |
| lweight | 0.263 | 0.316 | 0.238 | 0.169 | 0.289 | 0.344 |
| age | −0.141 | −0.046 | −0.152 | −0.026 | ||
| lbph | 0.210 | 0.162 | 0.002 | 0.214 | 0.220 | |
| svi | 0.305 | 0.227 | 0.094 | 0.315 | 0.243 | |
| lcp | −0.288 | 0.000 | −0.051 | 0.079 | ||
| gleason | −0.021 | 0.040 | 0.232 | 0.011 | ||
| pgg45 | 0.267 | 0.133 | −0.056 | 0.084 | ||
| ____________ | ________ | _____________ | ________ | ______ | ________ | ________ |
| Test Error | 0.521 | 0.492 | 0.492 | 0.479 | 0.449 | 0.528 |
| Std Error | 0.179 | 0.143 | 0.165 | 0.164 | 0.105 | 0.152 |
表 3.3:各种子集选择和收缩方法在前列腺癌症数据集上的估计系数和测试集误差结果。空白项意味这该变量被模型排除。
3.4.2 套索回归
套索回归(lasso)3与岭回归都属于收缩方法,两者有细微但重要的差别。套索回归的系数估计定义为:
$$\begin{align} \hat{\beta}^{\text{lasso}} &= \underset{\beta}{\arg\min} \sum_{i=1}^N (y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 \\ & \text{subject to} \sum_{j=1}^p |\beta_j| \leq t \end{align}\tag{3.51}$$与在岭回归中一样,在计算之前先对输入变量做标准化处理;截距 $\beta_0$ 的解即为 $\bar{y}$,在最小化问题中不再包含截距项,并将输出变量也做标准化处理。在最终拟合时,使用中心化后的输入和输出变量,不添加截距项。套索回归在信号处理领域(Chen et al. 1988)也被称为 基追踪(basis pursuit)。
套索回归的最小化也同样可以写成拉格朗日(Lagrangian)形式:
$$\hat{\beta}^{\text{lasso}} = \underset{\beta}{\arg\min} \left\{ \frac{1}{2} \sum_{i=1}^N (y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 + \lambda \sum_{j=1}^p |\beta_j| \right\}$$ $$\tag{3.52}$$注意到上面两种定义与岭回归的定义 3.42 和 3.41 的对比:$L_2$ 的岭惩罚项 $\sum_1^p\beta_j^2$ 被替换成了 $L_1$ 的套索惩罚项 $\sum_{1}^p|\beta_j|$。后者的约束条件使最小化问题的解不再是 $y_i$ 的线性转换,也因此不再像岭回归一样存在闭式解(closed form solution)。套索回归的解是一个二次规划(quadratic programming)问题,但第 3.4.4 节会介绍随 $\lambda$ 变动寻找整个解的路径的高效算法,使其计算成本与岭回归相当。套索回归约束的绝对值形式,使得当 $t$ 足够小时,一部分系数的估计会收缩到 0。从这个角度来说,套索回归实现了一种连续性的变量子集选择。当 $t$ 的值大于 $t_0=\sum_1^p|\hat{\beta}_j^{\text{ls}}|$(最小二乘系数估计的绝对值和),则套索回归与最小二乘回归的结果是一样的。当 t 的值为 $t_0/2$ 时,则套索回归的系数估计值大致为最小二乘的系数估计值的一半。不过套索回归的收缩性质并不如岭回归那样明确,第 3.4.4 节 会进行更深入的介绍。与变量子集选择的子集大小或岭回归中的惩罚参数类似,套索回归的 $t$ 也需要通过对期望预测误差估计的最小化来确定。
为了方便演示,图 3.7 中(左中)为套索回归的预测误差估计曲线,横轴为标准化的参数 $s=t/\sum_1^p|\hat{\beta}_j^{\text{ls}}|$。通过 10 次交叉验证,最终选取的参数为 $\hat{s}\approx0.36$;这使得四个系数取值为 0(表 3.3 中的第五列)。最终的模型的测试集误差比全变量的最小二乘模型稍小,在所有列出的模型中为第二低,但其测试集误差的标准误差(表 3.3 中的最后一行)仍然比较大。
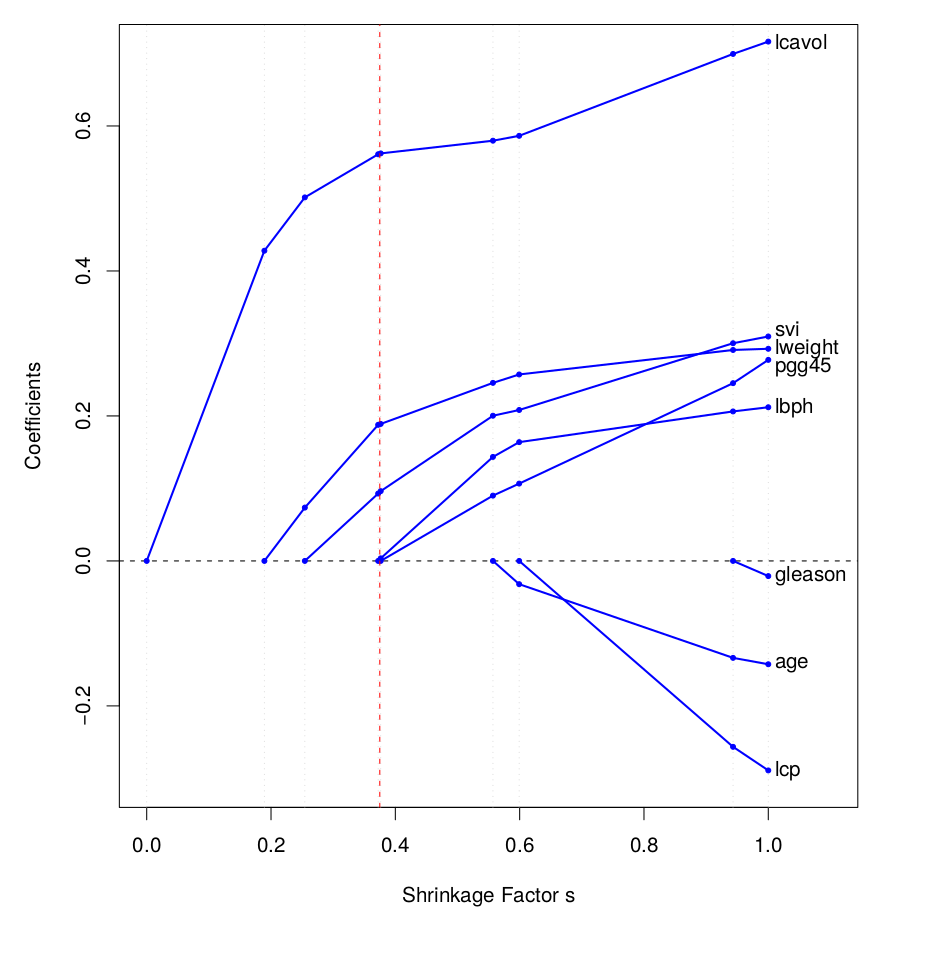
图 3.10 为套索回归的系数随标准化的调节参数 $s=t/\sum_1^p|\hat{\beta}_j^{\text{ls}}|$ 变化的曲线。在 $s=1.0$ 时,套索回归的系数等同于最小二乘回归;随着 $s\rightarrow0$,所有系数都向 0 收缩。在这个例子中,系数绝对值均为单调下降,但并不总是如此。竖线为通过交叉验证选取的 $s=0.36$。
3.4.3 对比:子集选择、岭回归、与套索回归
本节比较前文所介绍的三种有约束的线性回归模型:子集选择、岭回归、以及套索回归。
当输入变量矩阵 $\mathbf{X}$ 为标准正交矩阵时,三种方法均有显式的解,均为对最小二乘的系数估计 $\hat{\beta}_j$ 的某种转换,如表 3.4 所示。
| Estimator | Formula |
|---|---|
| Best subset (size M ) | $\hat{\beta}_j\cdot I(|\hat{\beta}_j|\geq|\hat{\beta}_{(M)}|)$ |
| Ridge | $\hat{\beta}_j/(1+\lambda)$ |
| Lasso | $\operatorname{sign}(\hat{\beta}_j)(|\hat{\beta}_j|-\lambda)_+$ |
表 3.4:标准正交矩阵 $\mathbf{X}$ 假设下的参数估计。$M$ 与 $\lambda$ 为通过相应的方法计算出的常数。$\operatorname{sign}(\cdot)$ 为其输入的符号函数($\pm1$),$x_+$ 为 $x$ 的“正部”。下图中,系数估计值为红色的虚线,45度灰色直线是作为参照的最小二乘的系数。

岭回归为按比例的收缩。套索回归将 0 点的邻域 $\lambda$ 内的值截断至 0,这种方式称为“软阈值(soft thresholding)”,在第 5.9 节的小波基函数平滑方法中也有使用。最优子集选择只保留最大的 $M$ 个系数,这种方式称为“硬阈值(hard thresholding)”。

一些图形可以帮助理解非正交矩阵时的系数变化。图 3.11 分别为套索回归(左图)和岭回归(右图)的二维系数空间。图中的椭圆的等值线为不同系数点对应的残差平方和,其中心为全变量的最小二乘的系数估计。岭回归的约束区域为一个圆形 $\beta_1^2+\beta_2^2\leq t$;拉索回归的约束区域为一个菱形 $|\beta_1|+|\beta_2|\leq t$。两个方法的解均为约束区域与最靠近中心点的等值线的切点。菱形与圆形不同,存在四个角,当切点出现在某个角上,则其中就产生了一个等于 0 的系数估计。当 $p>2$ 时,菱形区域变成了高维上的平行四边形,会有更多的角点,平的边缘和表面,也更容易产生含有 0 值的边界解。
岭回归和套索回归可以被视为贝叶斯估计方法,并推广为更广泛的方法。考虑下面的定义:
$$\tilde{\beta} = \underset{\beta}{\arg\min} \left\{ \sum_{i=1}^N (y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 + \lambda \sum_{j=1}^p |\beta_j|^q \right\}\tag{3.53}$$其中 $q\geq0$。图 3.12 展示了在二维参数空间上,约束区域的边界($\sum_j|\beta_j|^q$ 的等值线)。

如果将 $|\beta_j|^q$ 当作 $\beta_j$ 的对数先验概率密度函数,那么这些边界线也可以被当作参数的等似然程度曲线。在 $q=0$ 时,惩罚项即为非零参数的个数,对应着变量子集选择;在 $q=1$ 时,对应着套索回归;在 $q=2$ 时,对应着岭回归。注意在 $q\leq 1$ 时,先验密度在不同方向上的分布不平均,更集中于坐标轴的方向。当 $q=1$ 时,对数先验密度对应的正是独立双指数分布,或拉普拉斯(Laplace)分布,其密度函数为 $(1/2\tau)\exp(-|\beta|/\tau)$,令 $\tau=1/\lambda$。在这类估计方法中,能够保证约束区域为凸集(convex)的最小 $q$ 值为 1,即套索回归;在非凸约束区域上的最优化问题要更难计算。
从上面的角度来看,套索回归、岭回归、以及最优子集选择方法,均为使用了相应的先验概率密度函数的贝叶斯估计。然而需要注意的是,理论上它们的估计都是在寻找后验概率函数的众数,即最大化后验函数。但通常计算贝叶斯估计时使用的是后验函数的均值。对于岭回归来说,均值与众数一致;但对于其他的 $q$,包括套索回归和最优子集选择,并不如此。
除了 0、1、或 2 以外,我们也会尝试在定义 3.53 中的惩罚项中使用其他的 $q$ 值。虽然可能可以从数据中估计出合适的 $q$,但经验上这产生的额外的方差要大于带来的提升。在区间 $q\in(1,2)$ 上,对应的回归性质介于套索回归和岭回归之间。但是只要 $q>1$,$|\beta|^q$ 在 0 点可微,最终的解不会像套索回归一样产生等于 0 的系数估计。为了解决这个问题,以及更好地计算效率,(Zou and Hastie,2005)引入了弹性网络(elastic-net)惩罚项:
$$\lambda \sum_{j=1}^p (\alpha\beta_j^2 + (1-\alpha)|\beta_j|) \tag{3.54}$$这是另一种套索回归和岭回归的结合方式。图 3.13 比较了 $q=1.2$ 时的 $L_q$ 惩罚项和 $\alpha=0.2$ 的弹性网络惩罚项。以肉眼难以看出两者的区别。弹性网络方法像套索方法一样选择变量,并同时像岭回归一样对相关自变量的系数收缩。而且它比单纯的 $L_q$ 惩罚项在计算效率上更有优势。第 18.4 节会更详细介绍。

3.4.4 最小角回归
最小角回归(least angle regression, LAR) 是比较新的方法(Efron et al., 2004),可以看作是一种“民主”版本的前向逐步回归(第 3.3.2 节)。最小角回归与套索回归紧密相连,实际上它为计算如图 3.10 中的套索回归的系数路径曲线提供了一个效率极高的算法。
前向逐步回归通过每次添入一个变量而逐渐建立模型。在每一步,它在输入变量中寻找最佳的变量添加到模型中,最终再使用所有被选中的变量进行最小二乘拟合。
最小角回归的策略与之类似,但在每一步只将选中的变量的“部分”添加到模型中。首先找到与输出变量相关性最强的输入变量。最小角回归不会完全将这个变量加入到模型,而是将系数向量(初始化为长度为 p 的 0 向量)中对应的值向其最小二乘回归系数值连续地移动。相应地,系数向量的变化使得这个选中的输入变量与新残差向量的相关系数绝对值下降。随着其相关性的下降,逐渐会有另一个输入变量与新残差的相关系数绝对值与其相当,这一步的系数向量移动就结束了,并将新找到的输入变量加入到模型中。在下一轮的移动中,两个输入变量的系数同时移动,它们与残差的相关程度会保持一致并下降[5]。这个过程持续到所有的变量都被加入到模型中,结束时的拟合与最小二乘相同。算法 3.2 详细地描述了这个过程4。如果 $p>N-1$,则在 $N-1$ 步之后算法也会停止,因为最小角回归的残差会在 $N-1$ 步之后变为 0(其中减去 1 因为使用了中心化的数据)。
算法 3.2:最小角回归
- 初始化
- 将所有的输入变量向量标准化,均值为 0,范式(方差)为 1。
- 初始化残差为 $\mathbf{r}=\mathbf{y}-\bar{y}$,系数 $\beta_1$、$\beta_2$、……、$\beta_p$ 均为 0。
- 在输入变量中找到与残差 $\mathbf{r}$ 最相关的变量 $\mathbf{x}_j$。
- 第一步
- 此时模型中选入了一个输入变量,计算其当前的残差对这个变量的最小二乘估计值,$\langle\mathbf{x}_j,\mathbf{r}\rangle$。
- 将系数 $\beta_j$ 从 0 向最小二乘回归的估计值移动,而残差也随之相应地变动。
- 随着移动,比较所有输入变量与变化中的残差的相关程度,其趋势为 $\mathbf{x}_j$ 的相关程度从最高开始下降。
- 当出现某个其他变量 $\mathbf{x}_k$ 的相关性绝对值与 $\mathbf{x}_j$ 相同时,停止移动,将变量 $\mathbf{x}$ 加入到模型中。
- 第 k 步
- 计算 k 个变量的最小二乘系数估计。
- 系数从上一步移动停止时的结果向最小二乘系数估计移动,残差也随之变动。
- 随着移动,k 个变量与残差的相关性绝对值(相等)都会下降。
- 当某个未在模型中的变量的相关性绝对值与这 k 个变量相等,停止移动,并将其加入到模型。
- 持续上面这种流程,直到所有的 $p$ 个自变量都进入了模型。在经过 $\min(N-1,p)$ 步骤之后,即得到了全变量的最小二乘回归解。
假设 $\mathcal{A}_k$ 为在进入第 k 步时,已经被选中加入到模型的输入变量集合,$\beta_{\mathcal{A}_k}$ 为此时这些变量的系数向量5。这个向量中有 $k-1$ 个非零的值,和一个对应刚被加入的变量的 0 值。此时的残差为 $\mathbf{r}_k=\mathbf{y}-\mathbf{X}_{\mathcal{A}_k}\beta_{\mathcal{A}_k}$,第 k 步系数的移动方向为6:
$$\delta_k = (\mathbf{X}_{\mathcal{A}_k}^T\mathbf{X}_{\mathcal{A}_k})^{-1} \mathbf{X}_{\mathcal{A}_k}^T\mathbf{r}_k\tag{3.55}$$接下来,系数朝着这个方向移动:$\beta_{\mathcal{A}_k}(\alpha)=\beta_{\mathcal{A}_k}+\alpha\cdot\delta_k$。可以证明(练习 3.23)这种移动方式可以保证其中的所有输入变量与残差的相关程度保持相等并下降。如果在进入第 k 步时,模型的拟合为 $\hat{f}_k$,则在移动中对应的拟合为 $\hat{f}_k(\alpha)=\hat{f}_k+\alpha\cdot\mathbf{u}_k$,其中的 $\mathbf{u}_k=\mathbf{X}_{\mathcal{A}_k}\delta_k$ 为拟合移动的方向。最小角回归名字中的“最小角”来自于上述过程的几何含义。$\mathbf{u}_k$ 与所有 $\mathcal{A}_k$ 中的变量的夹角最小,并且角度相等(练习 3.24)。图 3.14 以模拟数据演示了最小角回归过程逐步递减的相关系数绝对值以及各个输入变量被添加到模型中的节点。


最小角回归的算法设计导致其系数的以分段线性的方式变化。图 3.15 的左边展示了最小角回归系数对其 $L_1$ 弧长7的变化图形。注意在算法的第 2.3 和 3.3 步骤中,并不需要不断对系数做小变动后计算相关性。利用算法分布线性的设计以及多变量协方差的性质,我们在每一步可以直接计算出移动将要停止的点的位置(练习 3.25)。
图 3.15 的右边展示了同样数据的套索回归系数的变化图形。它们几乎与左边的曲线一样,唯一不同是在深蓝色曲线的系数穿过 0 的那一段。在前列腺癌症数据中,最小角回归与图 3.10 中的套索回归系数系数变化曲线完全一致,注意其中的系数都没有穿过 0 点。实际上,对最小角回归进行一个简单的修正后,会得到同样为分段线性的套索回归的系数变化路径。
最小角(套索)回归算法极其高效,所需要的计算量与一个包含 p 个自变量的最小二乘拟合相当。最小角回归在经过 p 步之后总会得到最小二乘估计结果,而套索回归所需的步数可能会大于 p,但通常两者的路径会非常相似。在算法 3.2 加上针对套索回归的修正后,算法 3.2a 可以快速地计算套索回归的解,尤其是在 $p\gg N$ 的场景中。(Osborne et al,2000a)介绍了另一种分段线性方式的套索回归计算方法,称之为 同伦(homotopy) 算法。
算法 3.2a:最小角回归的套索修正
3.2a 当某个系数在移动中到达了 0 点,则从模型中排除该变量,将剩余的 $k-1$ 个变量的最小二乘估计作为移动方向,继续移动。
下面从解的条件来简单解释这两种回归方法如此相似的原因。最小角回归的计算中比较相关性,但如果输入特征变量经过了标准化处理,使用内积来的计算得到的结果相同并且更容易理解。假设算法在进入某一步时,已被选入模型的变量集合为 $\mathcal{A}$,所有变量与当前的残差 $\mathbf{y}-\mathbf{X}\beta$ 的内积绝对值都相等,可写为:
$$\mathbf{x}_j^T (\mathbf{y}-\mathbf{X}\beta) = \gamma \cdot s_j, \forall j \in \mathcal{A} \tag{3.56}$$其中的 $s_j\in\{-1,1\}$ 为内积的正负符号,$\gamma$ 则为所有内积的绝对值。同时有 $|\mathbf{x}_k^T(\mathbf{y}-\mathbf{X}\beta)|\leq\gamma,\forall k\notin\mathcal{A}$。将套索回归定义 3.52 中的目标函数用向量的形式写为:
$$R(\beta) = \frac{1}{2} \|\mathbf{y}-\mathbf{X}\beta\|_2^2 + \lambda \|\beta\|_1 \tag{3.57}$$给定 $\lambda$ 的值后,记 $\mathcal{B}$ 为解中所包含的变量的集合。则函数 $R(\beta)$ 针对这些变量可微,最小化问题的稳态条件为:
$$\mathbf{x}_j^T (\mathbf{y}-\mathbf{X}\beta) = \lambda \cdot \operatorname{sign}(\beta_j), \forall j \in \mathcal{B} \tag{3.58}$$当等式 3.58 中 $\beta_j$ 的符号与等式 3.56 中的内积的符号 $s_j$ 一致的时候,两个表达式是等价的。这也便是当某个被选入模型的变量系数通过 0 点时最小角回归和套索回归产生差异的原因,即这个变量不再满足 等式 3.58,在算法 3.2a 中会将其从集合 $\mathcal{B}$ 中去除。练习 3.23 会证明随着 $\lambda$ 下降,上式的条件会使系数解的路径呈分段线性。对于没有被加入模型的变量,必定满足稳态条件:
$$\mathbf{x}_k^T (\mathbf{y}-\mathbf{X}\beta) \leq \lambda, \forall j \in \mathcal{B} \tag{3.59}$$这又与最小角回归一致。

图 3.16 对比了最小角回归、套索回归、前向逐步回归和分段回归。数据生成机制与第 3.3 节中的图 3.6 一样,只是这里的 N 为 100 而不是 300,所以更难准确地拟合。可见作为贪心算法的前向逐步回归很快(在 10 个真实的输入变量都进入模型之前)即出现了过拟合,其最终的表现要优于收敛缓慢的前向分段回归。最小角和套索回归的表现与前向分段回归相似。第 3.8.1 节会介绍增量前向分段回归(incremental forward stagewise),其表现与最小角和套索回归相似。
最小角回归与套索回归的自由度
假设在使用最小角回归拟合线性模型的过程中,在某一步 $k<p$ 时,或类似地在套索回归中,对于某一个对系数的约束条件参数 $t$,如何定义此时模型中所包含的变量个数,或者“自由度(degrees of freedom)”?
首先考虑一个使用了 k 个输入特征变量的线性回归。如果这组变量为既定的,没有通过训练集进行任何筛选,则拟合模型使用的自由度即为 k。实际上在经典统计学中这正是“自由度”的含义,即模型中线性独立的参数个数。然而如果这 k 个变量是通过某个最优子集选择方法从更多的输入变量中选入模型的,那么虽然最终模型仍有 k 个参数,其实从某种程度来说最终模型使用的自由度要大于 k。
针对这种自适应拟合模型(adaptively fitted)8,需要定义更广义的有效自由度概念。对于某个输出变量拟合向量 $\hat{\mathbf{y}}=(\hat{y}_1,\hat{y}_2,\dots,\hat{y}_N)$,自由度定义为:
$$\operatorname{df}(\hat{\mathbf{y}}) = \frac{1}{\sigma^2} \sum_{i=1}^N \operatorname{Cov}(\hat{y}\_i,y_i) \tag{3.60}$$其中的 $\operatorname{Cov}(\hat{y}_i,y_i)$ 为预测值 $\hat{y}_i$ 与相应的真实输出变量 $y_i$ 的总体协方差9。直观上可以理解,模型拟合越接近样本数据,拟合值与真实值的协方差越大,因而自由度越大。等式 3.60 是很有用的自由度的定义方式,它可适用于任意模型的拟合 $\hat{\mathbf{y}}$,包括在训练数据集上的自适应拟合模型。第 7.4 节至第 7.6 节会深入理解这个定义。
对于固定 k 个自变量的线性回归,其自由度很容易计算为 $\operatorname{df}(\hat{\mathbf{y}})=k$。对于岭回归,通过定义可得到与式 3.50 一致的闭合表达式:$\operatorname{df}(\hat{\mathbf{y}})=\operatorname{tr}(\mathbf{S}_\lambda)$。这两个模型的拟合均为输出变量向量的线性转换 $\hat{\mathbf{y}}=\mathbf{H}_\lambda\mathbf{y}$,因此可以方便地推导出等式 3.60 的相应表达式。相反,对于最优子集选择方法,如果最终被选入模型的变量个数为 k,那么 $\operatorname{df}(\hat{\mathbf{y}})$ 的值会大于 k。可以直接通过计算模拟数据中的 $\operatorname{Cov}(\hat{y}_i,y_i)/\sigma^2$ 来验证此结论,但却无法推导出 $\operatorname{df}(\hat{\mathbf{y}})$ 的闭合表达式。
对于最小角和套索回归,到了见证奇迹的时刻。这两种方法的自适应方式要比最优子集选择更“平滑”,因而对自由度的估计也要容易一些。具体来说,可以证明在最小角回归进行了 k 步之后,拟合向量的有效自由度恰好为 k。对于套索回归,由于有时会从模型中排除变量,其(含修正的)最小角回归流程通常会大于 p 步。因此套索回归的自由度会稍有不同,在每一步中,$\operatorname{df}(\hat{\mathbf{y}})$ 近似于当前模型包含的自变量个数。这个近似在套索回归的系数路径上的任意位置都基本可以接受;而对算法流程中最后一个包含 k 个变量的模型,近似值与真实值很可能是一致的。关于套索回归自由度更详细的研究,可参考(Zou et al,2007)。
本节练习
练习 3.5
证明岭回归问题(式 3.41)与下面的问题是等价的。
$$\hat{\beta}^c = \underset{\beta^c}{\arg\min} \left\{ \sum_{i=1}^N [y_i - \beta_0^c - \sum_{j=1}^p(x_{ij}-\bar{x}_j)\beta_j^c]^2 + \lambda \sum_{j=1}^p {\beta_j^c}^2 \right\}$$ $$\tag{3.85}$$请给出 $\beta^c$ 和式 3.41 中的原 $\beta$ 之间的关系。 Characterize the solution to this modified criterion. 并证明套索(lasso)回归中也有类似的结果。
练习 3.6
Show that the ridge regression estimate is the mean (and mode) of the posterior distribution, under a Gaussian prior $\beta\sim\mathcal{N}(0,\tau\mathbf{I})$ and Gaussian sampling model $\mathbf{y}\sim\mathcal{N}(\mathbf{X}\beta,\sigma^2\mathbf{I})$ Find the relationship between the regularization parameter $\lambda$ in the ridge formula, and the variances $\tau$ and $\sigma^2$.
练习 3.7
假设 $y_i\sim\mathcal{N}(\beta_0+x_i^T\beta,\sigma^2)$,$i=1,2,\dots,N$ and the parameters $\beta_j, j=1,\dots,p$ are each distributed as $\mathcal{N}(0,\tau^2)$, independently of one another. Assuming $\sigma^2$ and $\tau^2$ are known, and $\beta_0$ is not governed by a prior (or has a flat improper prior), show that the (minus) log-posterior density of β is proportional to
$$\sum_{i=1}^N (y_i - \beta_0 - \sum_j x_{ij}\beta_j)^2 + \lambda \sum_{j=1}^p \beta_j^2$$where $\lambda=\sigma^2/\tau^2$.
练习 3.8
Consider the QR decomposition of the uncentered $N\times(p+1)$ matrix X (whose first column is all ones), and the SVD of the $N\times p$ centered matrix X̃. Show that Q 2 and U span the same subspace, where Q 2 is the sub-matrix of Q with the first column removed. Under what circumstances will they be the same, up to sign flips?
练习 3.16
Derive the entries in Table 3.4, the explicit forms for estimators in the orthogonal case.
练习 3.23
Consider a regression problem with all variables and response having mean zero and standard deviation one. Suppose also that each variable has identical absolute correlation with the response:
$$\frac{1}{N} |\langle \mathbf{x}\_j, \mathbf{y} \rangle| \lambda, j=1,\dots,p$$Let β̂ be the least-squares coefficient of y on X, and let u(α) = αX β̂ for α ∈ [0, 1] be the vector that moves a fraction α toward the least squares fit u. Let RSS be the residual sum-of-squares from the full least squares fit.
- Show that $$\frac{1}{N} |\langle \mathbf{x}\_j, \mathbf{y}-\mathbf{u}(\alpha) \rangle | \lambda, j = 1, \dots, p$$ and hence the correlations of each x j with the residuals remain equal in magnitude as we progress toward u.
- Show that these correlations are all equal to $$\lambda(\alpha) = \frac {(1-\alpha)} {\sqrt{(1-\alpha)^2 + \frac{\alpha(2-\alpha)}{N} \cdot \text{RSS}}} \cdot\lambda$$ and hence they decrease monotonically to zero.
- Use these results to show that the LAR algorithm in Section 3.4.4 keeps the correlations tied and monotonically decreasing, as claimed in (3.55).
练习 3.24
LAR directions. Using the notation around equation (3.55) on page 74, show that the LAR direction makes an equal angle with each of the predictors in A k .
练习 3.25
LAR look-ahead (Efron et al., 2004, Sec. 2). Starting at the beginning of the kth step of the LAR algorithm, derive expressions to identify the next variable to enter the active set at step k + 1, and the value of α at which this occurs (using the notation around equation (3.55) on page 74).
练习 3.28
Suppose for a given t in (3.51), the fitted lasso coefficient for variable Xj is β̂j = a. Suppose we augment our set of variables with an identical copy Xj∗ = Xj . Characterize the effect of this exact collinearity by describing the set of solutions for β̂j and β̂j∗ , using the same value of t.
练习 3.29
Suppose we run a ridge regression with parameter λ on a single variable $X$, and get coefficient $a$. We now include an exact copy $X^*=X$, and refit our ridge regression. Show that both coefficients are identical, and derive their value. Show in general that if m copies of a variable $X_j$ are included in a ridge regression, their coefficients are all the same.
-
与之相比,最小二乘则不会被输入变量的缩放/测量单位所影响。 ↩︎
-
这里的是紧奇异值分解(compact SVD),而不是完全形式的奇异值分解。 ↩︎
-
lasso 一词为 least absolute shrinkage and selection operator 的首字母缩写,直译为“最小绝对值收缩和选择算子”。中文维基和百度搜索中都存在“套索”的译法,虽然在实际中大家似乎都直接使用 lasso 一词,但在此系列中会保持使用术语的中文。但“拉索”是不是更贴切? ↩︎
-
这里描述的算法与原文的差异较大,因为原文过于简略,译者在理解时比较吃力。 ↩︎
-
维度为 $k\times1$。 ↩︎
-
$\mathbf{X}_{\mathcal{A}_k}$ 为只包含 $\mathcal{A}_k$ 中的变量的输入变量矩阵,其列维度等于集合 $\mathcal{A}_k$ 中变量的个数。 ↩︎
-
原文脚注2:某个定义在 $s\in[0,S]$ 上的可微曲线 $\beta(s)$ 的 $L_1$ 弧长为:$\operatorname{TV}(\beta,S)=\int_0^S|\dot{\beta}(s)|_1ds$,其中 $\dot{\beta}(s)=\partial\beta(s)/\partial s$。在分段线性的最小角回归系数曲线中,这个长度的含义为每一步系数线性移动的 $L_1$ 范式的和。 ↩︎
-
自适应拟合(adaptively fitted)模型,译者的理解是这种模型会主动地根据训练集的数据来决定本身的回归方程,例如最优变量子集选择方法。 ↩︎
-
原文为“sampling covariance”,译者理解指的是“population covariance”。 ↩︎