目前我们已经讨论了两个统计学习方法:稳定但偏差大的线性模型,和不稳定但偏差小的 k 最近邻方法。而且我们说明了只要训练样本足够多,则对于任意点 $x$ 其最近邻域的都可以足够靠近且有足够多的点,所以用 k 最近邻方法可以很好地用邻域上的平均来近似理论上的最优条件期望。然而在高维度的场景中,这个方法不再可行,这个现象常被称为 维数灾难(curse of dimensionality),(Bellman,1961)。高维度问题呈现的形式有很多,接下来我们用几个例子来说明。

假设输入变量为在 $p$ 维度空间上的标准均匀分布,即均匀分布在 $p$ 维空间上的单元超立方体(unit hypercube)中。我们想要获取某个点周末的一个超立方体邻域,使得其中包含的点占样本整体的比例为 $r$。这个比例相当于对应着这个邻域在这个单元超立方体所占的“体积”,因此其对应的“边长”尺度为 $e_p(r)=r^{1/p}$。在 10 维度空间中,计算可得 $e_p(0.01)=0.63$,$e_p(0.1)=0.8$,而均匀分布的单元超立方体的范围的边界长为 1。换句话说,要用整体样本的 1% 或 10% 形成的邻域样本取局部平均,就需要选取输入向量每个维度的 63% 或 80% 的范围。但如此的邻域已经不再体现这个点的局部特征了。采用特别小的比例 $r$ 也不会解决这个问题,因为如果邻域中的样本太少,又会带来过高的方差。
高维度中的稀疏样本问题,同时又导致了样本会更向输入变量空间的边缘集中。考虑均匀分布在 $p$ 维度空间上以原点为中心的单位球体中的 $N$ 个样本点。若想要获得模型在原点上的估计,我们需要获得原点附近的最近邻域。所有样本点与原点距离的中位数为(练习 2.3):
$$d(p,N) = \left( 1 - (\frac{1}{2})^{1/N} \right) ^{1/p} \tag{2.24}$$样本点与原点距离的均值的表达式要比中位数更复杂。根据上式,当 $N=500$,$p=10$,距离中位数为 $d(p,N)\approx0.52$,大于单位球体的“半径”的一半。可见对大多数的点来说,样本空间的边界要比其他的样本点更临近1。样本空间内部的点可以用插值(intropolate),而边界附近的点可能需要外推(extrapolate)来估计,相对于插值,外推的结果意义更小,不稳定。这给模型预测带来了困难。
维数灾难的另一个表现形式是取样密度,在 $p$ 维度的输入变量空间上,样本量为 $N$,则取样密度与 $N^{1/p}$ 成正比。想要达到在一维输入变量空间中 $N_1=100$ 的样本量一样的取样密度,在 10 维度输入变量空间上所需要的样本量数量级为 $N_{10}=100^{10}$。这是不太可能实现的,因此在高维度问题中,几乎所有可得的训练样本都是输入变量空间上的稀疏采样。
接下来我们用另一个均匀分布来示例。假设有 1000 个服从 $[-1,1]^p$ 上均匀分布的样本 $x_i$,真实的 $X$ 和 $Y$ 之间的方程关系为:
$$Y = f(X) = e^{-8 \|X\|^2}$$现使用 1 最近邻方法来预测在 $x_0=0$ 点处对应的 $y_0$。将训练集记为 $\mathcal{T}$。重复这个样本生成过程,然后将结果取平均,会得到在 $x_0$ 点上的期望预测误差的一个估计。由于输出变量与输入变量为确定的函数关系2,$f(0)$的估计的均方误差可以写为:
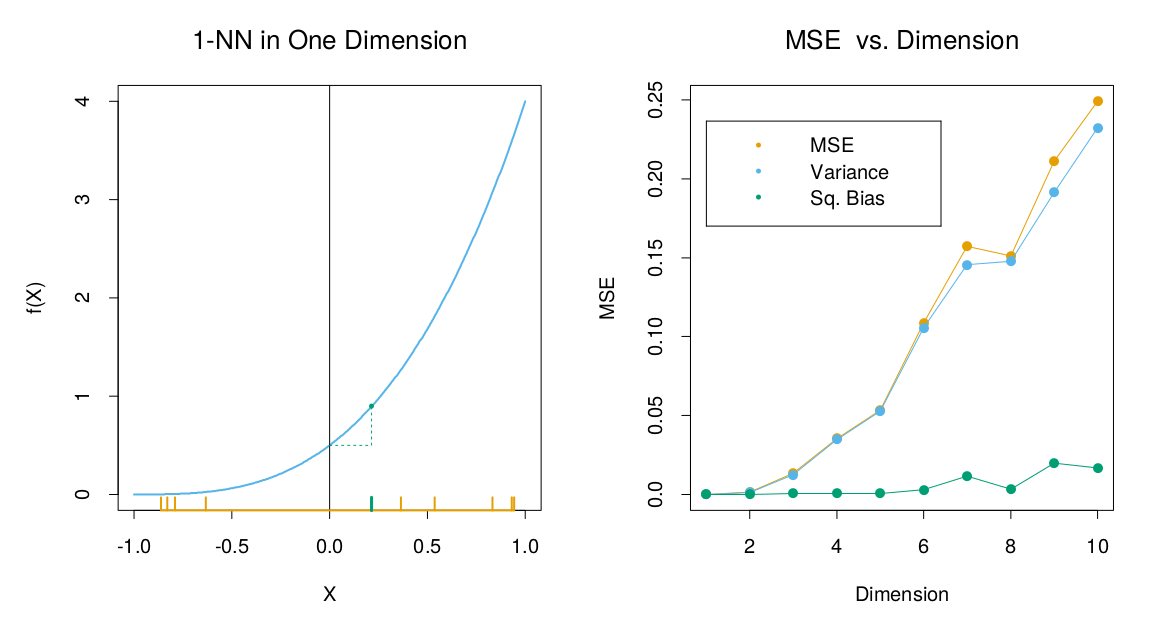
$$\begin{align} \operatorname{MSE}(x_0) &=\operatorname{E}_{\mathcal{T}} [f(x_0) - \hat{y}_0]^2 \\ &=\operatorname{E}_{\mathcal{T}} [\hat{y}_0 - \operatorname{E}_{\mathcal{T}}(\hat{y}_0)]^2 + [\operatorname{E}_{\mathcal{T}}(\hat{y}_0) - f(x_0)]^2 \\ &=\operatorname{Var}_{\mathcal{T}}(\hat{y}_0) + \operatorname{Bias}^2(\hat{y}_0) \tag{2.25} \end{align}$$![**图 2.7**:用于说明维数灾难和其对 MSE、偏差和方差的影响的模拟数据示例。输入变量特征在 $[-1,1]^p, p=10$ 上均匀分布。左上图为真实的取值在 $\mathbb{R}$ 上的输出函数 $f(X)=e^{-8\|X\|^2}$,其中一个蓝色的标记为原点的最近邻域点,图中显示了对应的 1 最近邻预测的偏差。右上图用一维和二维空间展示了当维度增加时 1 最近邻的范围也会增加。左下图为维度与 1 最近邻的平均半径的关系。右下图为维度与 MSE、平方偏差和方差的关系。](https://public.guansong.wang/eslii/ch02/eslii_fig_02_07.png)
图 2.7 表现了这个示例。MSE 被分解成了两个组成部分:方差项和平方误差项。这种对 MSE 的分解总是存在的,即为所谓的 偏差方差分解(bias-variance decomposition),而且经常有助于理解,在之后会经常使用。在这个例子中,除非样本中存在 0 点,否则 $\hat{y}_0$ 总是小于真实值 $f(0)$,3 因此模型的估计值是下偏的。在低维度且样本量 $1000$ 的情况下,$x_0$ 点的最近邻域十分接近于 0,故偏差和方差都很小。随着空间维度的增加,这个最近邻域会越来越远离目标点,偏差和方差均会增加4。当维度 $p = 10$ 时,99% 以上的样本点的最邻近样本点都与原点的距离大于 0.5。因而随着 $p$ 的增加,模型的预测会非常偏向于 0,因此 MSE 和偏差会趋向于 1.0,而相反方差会下降(这是由这个例子的设计所导致)。
虽然以上是一个经过设计的例子,但类似的现象确实广泛存在。一个多输入参数的方程的复杂度可能会随着维度增加而指数级地增加,如果我们想要达到和低维度方程同样的拟合准确度,则所需的训练样本量也要指数级地增加。在上例中,方程使用到了所有的 $p$ 个输入变量。
不同的情景下,偏差对模型预测的准确度影响不同,在 1-近邻方法中偏差项也并不总是主导着 MSE。5 例如图 2.8,如果真实的方程只涉及较低维度输入变量,则方差项主导了 MSE。
另一方面,若假设我们知道真实的输入输出变量的关系为线性方程:
$$Y = X^T \beta + \varepsilon \tag{2.26}$$其中的扰动项 $\varepsilon\sim\mathcal{N}(0,\sigma^2)$。我们在训练样本上用最小二乘法来拟合模型。对于任意一个测试点 $x_0$,模型的预测为 $\hat{y}_0=x_0^T\hat{\beta}$,也可写为 $\hat{y}_0=x_0^T\beta+\sum_{i=1}^N\ell_i(x_0)\varepsilon_i$,这里的 $\ell_i(x_0)$ 为向量 $X(X^TX)^{-1}x_0$ 的第 i 个元素。在线性模型中,最小二乘法是无偏的,所以:
$$\begin{align} \operatorname{EPE}(x_0) &=\operatorname{E}_{y_0|x_0} \operatorname{E}_{\mathcal{T}}(y_0 - \hat{y}\_0)^2 \\ &=\operatorname{Var}(y_0|x_0) + \operatorname{E}_{\mathcal{T}}[\hat{y}_0-\operatorname{E}_{\mathcal{T}}\hat{y}\_0]^2+ [\operatorname{E}_{\mathcal{T}}\hat{y}_0-x_0^T\beta]^2 \\ &=\operatorname{Var}(y_0|x_0) + \operatorname{Var}_{\mathcal{T}}(\hat{y}_0)+ \operatorname{Bias}^2(\hat{y}_0)\\ &=\sigma^2 + \operatorname{E}_{\mathcal{T}}x_0^T(X^TX)^{-1}x_0\sigma^2+0^2 \end{align}$$ $$\tag{2.27}$$由于输出变量的函数中存在不确定的扰动项,在 MSE 中有一个额外的方差项 $\sigma^2$。偏差项为 0,方差项依赖于 $x_0$。当 $N$ 足够大且样本 $\mathcal{T}$ 为随机选取,假设 $\operatorname{E}(X)=0$,则 $X^TX\rightarrow N\operatorname{Cov}(X)$,并且:
$$\begin{align} \operatorname{E}_{x_0} \operatorname{EPE}(x_0) &\sim \operatorname{E}_{x_0} x_0^T \operatorname{Cov}(X)^{-1}x_0 \sigma^2/N + \sigma^2 \\ &= \operatorname{trace}[\operatorname{Cov}(X)^{-1}\operatorname{Cov}(x_0)] \sigma^2/N + \sigma^2 \\ &= \sigma^2 (p/N) + \sigma^2 \tag{2.28}\end{align}$$可见在对 EPE 取期望后,是一个关于维度 $p$ 的线性方程,斜率为 $\sigma^2/N$。如果 $N$ 很大并且/或者 $\sigma^2$ 很小,则方差随维度的增加可以忽略(在无扰动项时方差为 0)。这样我们通过对模型的结构加上比较强的假设条件规避了维数灾难。练习 2.5 推导了等式 2.27 和 2.28 的部分步骤。

图 2.9 在两个场景中比较了 1 最近邻方法和最小二乘法。输入变量的模拟方法与图 2.7 中相同,样本大小为 $N=500$。两个场景的输出变量函数都为 $Y=f(X)+\varepsilon$ 的形式,$\varepsilon\sim\mathcal{N}(0,1)$,只是 $f(X)$ 不同:橙色曲线的 $f(X)$ 为第一个输入变量的线性方程,蓝色曲线为如图 2.8 中的三次方程。曲线展示的是 1 最近邻方法和最小二乘的 EPE 比值。在线性关系的橙色曲线中,左侧的比值大概为 2,此时最小二乘法是无偏的,而且如上所述它的 EPE 略高于 $\sigma^2=1$。1 最近邻的 EPE 总是高于 2,因为在这个例子中输出函数中包含了扰动项,而且随着维度的增加,近邻的半径逐渐扩大,橙色曲线的值也在增大。在三次方关系的蓝色曲线中,最小二乘法不再是无偏估计,所以降低了比值。如果我们设计的例子使得偏差项远大于方差项,那么结果会使 1 最近邻表现优于最小二乘法。
线性模型通过严格的假设,得到了无偏和低方差的结果,而 1 最近邻方法的偏差很大。然而,如果假设不成立,则这个结论不再成立,1 最近邻可能更优。介于严格强假设的线性模型和极度灵活的 1 最近邻方法之间,存在更多采用不同程度的假设和偏差的各种模型,这些模型的出发点都是通过某种假设来避免高维度问题中回归方程指数级增长的复杂度。
在深入这些模型前,下一节会在模型预测的框架下,从宏观的角度理解统计模型。
本节练习
练习 2.3
推导表达式 2.24。
练习 2.4
第 23 页中讨论的边界效应问题并不是在有界区域内的均匀分布样本所特有的。考虑服从一个球状的多元正态分布的一组输入变量 $X\sim\mathcal{N}(0,\mathbf{I}_p)$。任一样本点到原点的距离平方服从一个均值 $p$ 的卡方分布 $\chi_p^2$。考虑一个从这个分布中生成的预测点 $x_0$,并令 $a=x_0 / \|x_0\|$ 为对应的单位向量。令 $z_i=a^T x_i$ 为每个训练样本点在这个方向上的投影。
解 2.4
$z_i$ 服从分布 $\mathcal{N}(0,1)$,其到原点的距离平方的期望为 $1$,而目标点到原点的距离平方的期望为为 $p$。
因此,若 $p=10$,一个随机抽取的测试点与原点之间的标准差大概为 3.1,而所有训练样本在方向 $a$ 上的标准差的平均为 1。所以,大部分的预测点可视为落在了训练集的边界附近。
练习 2.5
- 推导表达式 2.27。The last line makes use of (3.8) through a conditioning argument.
- 推导表达式 2.28。making use of the cyclic property of the trace operator [trace(AB) = trace(BA)], and its linearity (which allows us to interchange the order of trace and expectation).